Advanced Engineering Dynamics

1.

1. Find the angular velocity reached by frame 1 at time \(t_1\text{.}\)
2. Find the work done by the frictional forces between 1 and 2 from time \(t=0\) to time \(t= t_1\text{.}\) Verify that this work is negative.

2.

• Body 1 is a torus-shaped body, of homogeneous density, center \(O\text{,}\) radius \(R\text{,}\) and mass \(m_1\text{.}\) A basis attached to 1 is \(b_1 (\bx_1,\by_1,\bz_1= \bz_0)\) as defined in the figure. The plane \((O, \bx_1, \bz_1)\) is a plane of symmetry. It is connected to frame 0 by an ideal pivot of axis \((O,\bz_0)\text{,}\) and its position is defined by angle \(\psi = (\bx_0,\bx_1)= (\by_0 ,\by_1)\text{.}\) Denote by \(I_1\) the moment of inertia of body 1 about axis \((O,\bz_0)\text{.}\)
• Body 2 is a truncated hollow torus-shaped body of mass center \(G\text{,}\) mass \(m_2\text{,}\) and basis \(b_2 (\bx_2 ,\by_2 = \by_1 ,\bz_2 = \bx_2\times \by_2)\) such that \(\br_{OG}= R \bx_2\text{.}\) The external surface of 1 is in contact with the internal surface of 2: body 2 is free to “slide” relative to 1, and its motion relative to 1 is entirely parametrized by angle \(\theta = (\bx_1 , \bx_2) = (\bz_0, \bz_2)\text{.}\) Its inertia operator about \(G\) is represented by:

  \begin{equation*} [\cI_{G, 2}]_{b_2} = \begin{bmatrix} A_2 \amp 0 \amp 0 \\ 0 \amp B_2 \amp 0 \\ 0 \amp 0 \amp C_2 \end{bmatrix}_{b_2} \end{equation*}

  The direct contact between 1 and 2 is assumed frictionless. The corresponding contact action screw \(\{\cA_{1\to 2}^c \}\) must satisfy the condition

  \begin{equation*} \bM_{O, 1\to 2}^c \cdot \by_1 = 0 \end{equation*}

  A motor \(\cal M\) is mounted between 0 and 1, and imposes a prescribed angle \(\psi (t)\text{.}\) The action of \(\cal M\) on 1 is equivalent to a couple \(\cC \bz_0\text{.}\) All aerodynamics effects are neglected.

1. Justify the form of inertia matrix \([\cI_{G, 2}]_{b_2}\text{.}\)
2. Derive the two equations extracted from the Fundamental Theorem of Dynamics in order to find the unknown couple \(\cC\) and angle \(\theta (t)\text{.}\)
3. Apply the Kinetic Energy Theorem to system \(\Sigma\text{.}\) How is this result related to the equations derived in b.?

Solution.

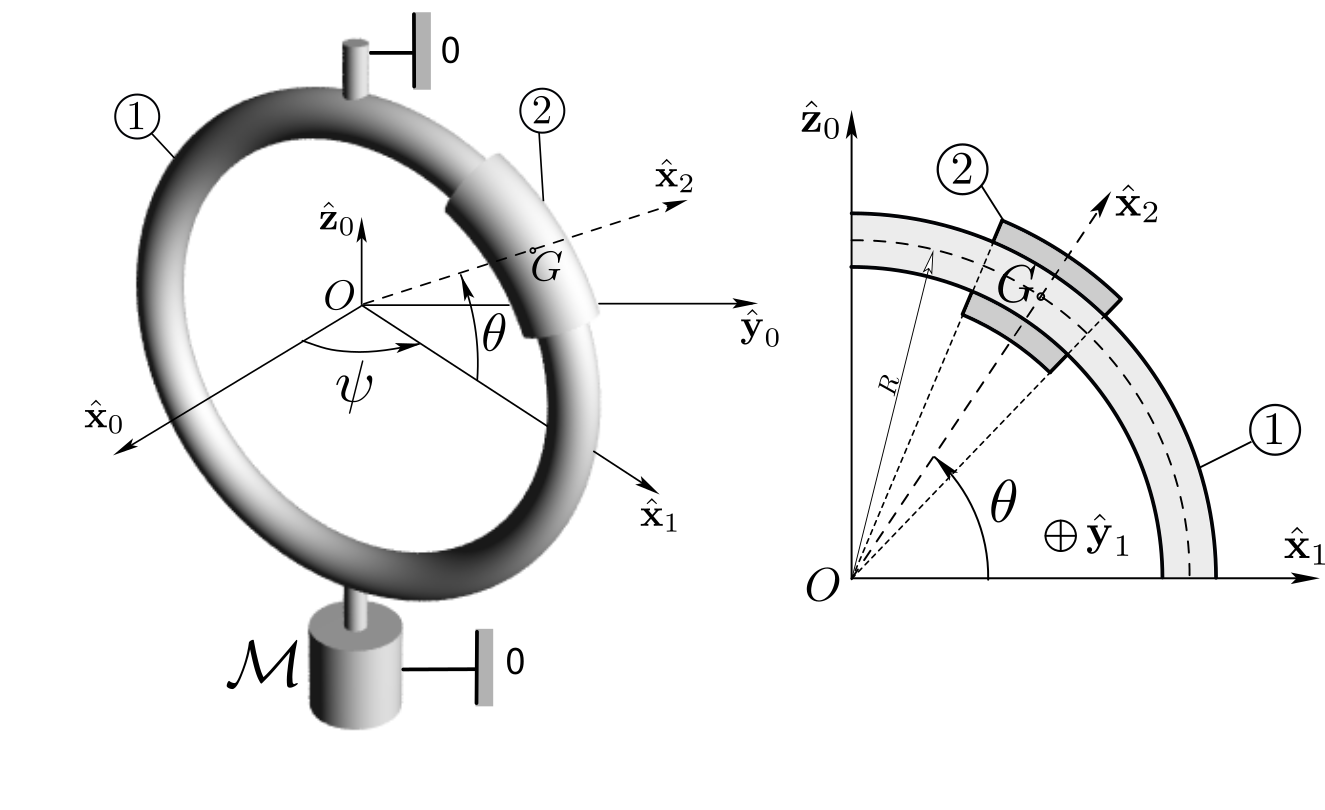
a. The form of inertia matrix \([\cI_{G,2}]_{b_2}\) on basis \(b_2 (\bx_2, \by_2 = \by_1 , \bz_2)\) can be justified by examining the symmetries of body 2: two plane symmetries can be found, the symmetry w.r.t. plane \((G, \bx_2 ,\bz_2)\) and the symmetry w.r.t. plane \((G, \bx_2 ,\by_1)\text{.}\) All products of inertia must be zero on this basis. We expect \(A_2 \neq B_2 \neq C_2\text{.}\)

b. We sketch a diagram showing all interconnections/interactions. We also sketch the rotation diagrams for convenience. See Figure 12.8.3.

The two equations extracted from the FTD are found by exploiting the two specific vanishing components of the contact actions screws \(\{\cA_{0\to 1} \}^c\) and \(\{\cA_{1\to 2} \}^c\text{:}\)

\begin{equation*} \bM_{O, 0\to 1}^c \cdot \bz_0 =0, \qquad \bM_{O, 1\to 2}^c \cdot \by_1 =0 \end{equation*}

The first equation is found by applying

\begin{equation*} \bM_{O, \bSi\to \Si}^c \cdot \bz_0 = \bD_{O, \Si/0}\cdot \bz_0 = \cC \end{equation*}

This causes all actions internal to system \(\Sigma\) to vanish. The contribution of gravity also vanishes.

For the second equation, we apply the FTD on body 2 as follows:

\begin{equation*} \bM_{O, \bar{2}\to 2}^c \cdot \by_1 = \bD_{O, 2/0}\cdot \by_1 \end{equation*}

For the first equation, we find the \(z_0\) component of dynamic moment \(\bD_{O, \Sigma /0}\) as follows:

\begin{equation*} \bD_{O, \Si/0}\cdot \bz_0 = \bD_{O, 1/0}\cdot \bz_0 + \bD_{O, 2/0}\cdot \bz_0 = \frac{d}{dt}\left( \bH_{O, 1/0}\cdot \bz_0 + \bH_{O, 2/0}\cdot \bz_0 \right) \end{equation*}

with \(\bH_{O, 1/0}\cdot \bz_0 = I_1 \dpsi\text{.}\) Angular momentum \(\bH_{O, 2/0}\) of body 2 about \(O\) is found from angular momentum \(\bH_{G, 2/0}\) about \(G\)

\begin{equation*} \bH_{O, 2/0}\cdot \bz_0 = (\bH_{G, 2/0}+ \br_{OG}\times m_2 \vel_{G/0})\cdot \bz_0 \end{equation*}

using velocity

\begin{equation*} \vel_{G/0} = d(R\bx_2)/dt = R(\dpsi \cos \te \by_1 + \dte \bz_2) \end{equation*}

and angular momentum

\begin{equation*} \bH_{G, 2/0} = \cI_{G,2}(\bom_{2/0}) = A_2 \dpsi \sin\te \bx_2 -B_2\dte \by_1 + C_2 \dpsi \cos\te \bz_2 \end{equation*}

So we find

\begin{equation*} \bH_{O, 2/0} = A_2 \dpsi \sin\te \bx_2 -(B_2+mR^2) \dte \by_1 + (C_2+mR^2) \dpsi \cos\te \bz_2 \end{equation*}

Note that this last result could be found by find operator $\cI_{G,2}$ with the parallel axis theorem. Now we can find the \(\bz_0\) component:

\begin{equation*} \bH_{O, 2/0} \cdot \bz_0 = [ A_2 \sin^2 \te + (C_2 +m_2 R^2) \cos^2 \te]\dpsi \end{equation*}

finally leading to equation

\begin{equation*} \boxed{ \frac{d}{dt}\left[ I_1 + A_2 \sin^2 \te + (C_2 +m_2 R^2) \cos^2 \te\right]\dpsi = \cC } \qquad{(1)} \end{equation*}

For the second equation, we can express dynamic moment \(\bD_{O , 2/0} \cdot \by_1\) as

\begin{equation*} \bD_{O , 2/0} \cdot \by_1 = \frac{d}{dt} \left( \by_1 \cdot \bH_{O , 2/0} \right) + \dpsi \bx_1 \cdot \bH_{O, 2/0} = \bM_{O, \bar{2}\to 2}^c \cdot \by_1 = m_2 gR\cos\te \end{equation*}

This avoids seeking all components of \(\bD_{O , 2/0}\text{.}\) We find

\begin{equation*} \by_1 \cdot \bH_{O , 2/0} = - (B_2 +m_2 R^2) \dte \end{equation*}

and

\begin{equation*} \bx_1 \cdot \bH_{O, 2/0} = (A_2 -C_2-m_2R^2) \dpsi \sin\te\cos\te \end{equation*}

This leads to the second equation:

\begin{equation*} \boxed{ - (B_2 +m_2 R^2) \ddte + (A_2 -C_2-m_2 R^2) \dpsi^2 \sin\te\cos\te = m_2 gR\cos\te} \qquad{(2)} \end{equation*}

c. To apply the KET to system \(\Si\) we write

\begin{equation*} \frac{d}{dt} (\kin_{1/0}+ \kin_{2/0}) = \Pow_{\bSi \to \Si /0} + \Pow_{1\leftrightarrow 2} \end{equation*}

with kinetic energies

\begin{equation*} \kin_{1/0}= \half I_1 \dpsi^2 \end{equation*}

and

\begin{align*} \kin_{2/0} \amp = \half m_2 \vel_{G/0}^2 + \half \bom_{2/0} \cdot \bH_{G, 2/0}\\ \amp = \half m_2 R^2 (\dte^2 + \dpsi^2 \cos^2 \te) + \half (A_2 \dpsi^2 \sin^2 \te + C_2 \dpsi^2 \cos^2 \te + B_2 \dte^2). \end{align*}

Since the joint \(0\leftrightarrow 1\) is ideal, we have \(\Pow^c_{0\leftrightarrow 1} =0\) leading to the expression of total external power

\begin{equation*} \Pow_{\bSi \to \Si /0} = \cC \dpsi - m_2 g R \dte \cos\te \end{equation*}

Also internal power \(\Pow^c_{1\leftrightarrow 2}\) vanishes, since the joint \(1\leftrightarrow 2\) is ideal. This gives the final equation

\begin{equation*} \boxed{ \frac{d}{dt} \left\{ \half(m_2 R^2 +B_2)\dte^2 + \half (I_1 + A_2 \dpsi^2 \sin^2 \te + C_2 \dpsi^2 \cos^2 \te + m_2 R^2 \cos^2\te)\dpsi^2 \right\} = \cC \dpsi - m_2 g R \dte \cos\te } \end{equation*}

We know that the KET applied to system \(\Si\) is equivalent to the sum of following equations

\begin{equation*} \{\cA_{ \bar{1}\to 1} \} \cdot \{ \cV_{1/0} \} = \{ \cD_{1/0} \}\cdot \{ \cV_{1/0} \} \qquad{(3)} \end{equation*}

\begin{equation*} \{\cA_{ \bar{2}\to 2} \} \cdot \{ \cV_{2/0} \} = \{ \cD_{2/0} \}\cdot \{ \cV_{2/0} \} \qquad{(4)} \end{equation*}

with the kinematic screws given by

\begin{equation*} \{ \cV_{2/0} \} = \left\{ \begin{array}{c} (\dpsi \bz_0 -\dte \by_1) \\ \bze \end{array} \right\}_O \qquad \{ \cV_{1/0} \} = \left\{ \begin{array}{c} \dpsi \bz_0 \\ \bze \end{array} \right\}_O \end{equation*}

We add equations (3) and (4) to get

\begin{equation*} \dpsi \bz_0 \cdot \bM_{O, \bar{1}\to 1} + (\dpsi \bz_0 -\dte \by_1) \cdot \bM_{O, \bar{2}\to 2} = \dpsi \bz_0 \cdot \bD_{O, 1/0}+ (\dpsi \bz_0 -\dte \by_1) \cdot \bD_{O, 2/0} \end{equation*}

It is now easy to see that the KET applied to system \(\Si\) is equivalent to

\begin{equation*} \boxed{ (1) \times \dpsi + (2) \times (-\dte) = 0 } \end{equation*}