Section 1.1 Parametrization of the Position a Rigid Body
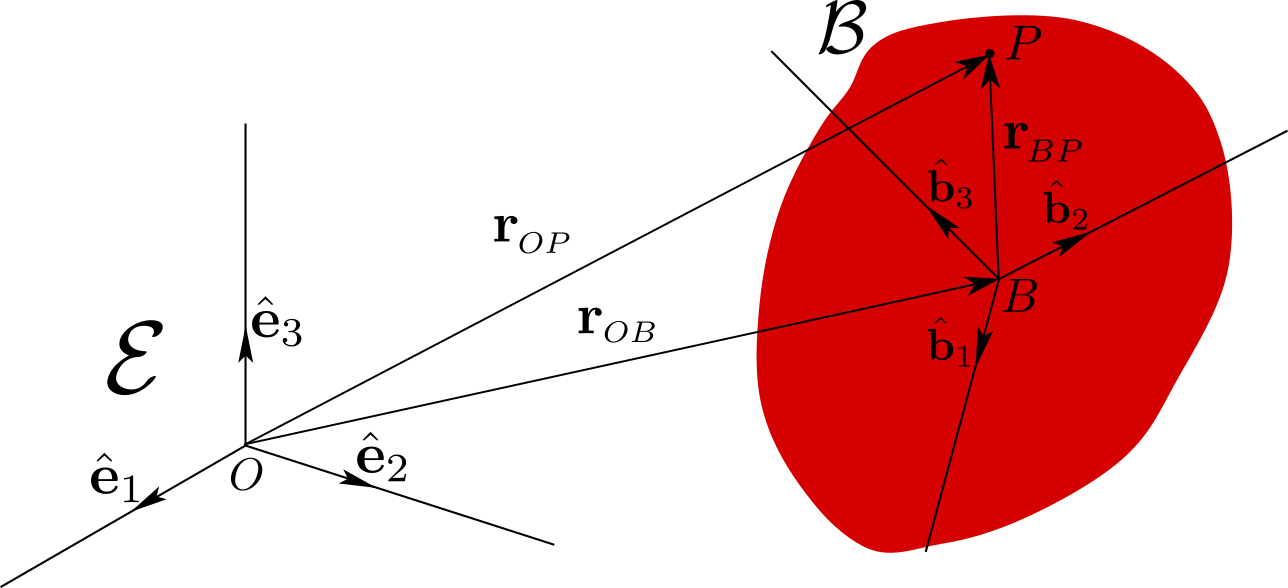
In mechanics, motions are observed relative to a referential \(\cE\text{,}\) that is, a Euclidean physical space (There is a one-to-one mapping between \(\cE\) and \(\mathbb{R}^3\) once an origin of \(\cE\) is chosen.). A particular point \(O\) of \(\cE\) is chosen to define an origin of \(\cE\text{.}\) Referential \(\cE\) is also equipped with an orthonormal right-handed basis \((\be_1,\be_2,\be_3)\text{.}\) All orthonormal bases, whether fixed or mobile, will always be chosen right-handed. A rigid body \(\cB\) is a mathematical abstraction, defined as a connected subset of points which remain at a constant distance from each other. Body \(\cB\) is equipped with an orthonormal right-handed basis \((\bhb_1,\bhb_2,\bhb_3)\) which remains attached to \(\cB\) at all time. An origin \(B\) of \(\cB\) is chosen as a point fixed in \(\cB\) at all time. In this chapter, we seek to parametrize the position of \(\cB\) relative to \(\cE\text{,}\) that is, to define a set of parameters which would enable us to find the positions of all points attached to \(\cB\) relative to \(\cE\text{.}\) Since body \(\cB\) is rigid, this requires a parametrization of the set \((B, \bhb_1,\bhb_2,\bhb_3)\) relative to the set \((O,\be_1,\be_2,\be_3)\text{:}\) indeed the position of an arbitrary point \(P\) attached to \(\cB\) relative to \(\cE\) is defined by the equation \(\br_{OP}= \br_{OB}+\br_{BP}\) as seen in Figure 1.1.1.
Defining the position of \(\cB\) relative to \(\cE\) is then equivalent to:
- (i) defining the position of origin \(B\) in \(\cE\text{,}\) thus allowing for the determination of position vector \(\br_{OB}\text{,}\)
- (ii) defining the orientation of basis \((\bhb_1 , \bhb_2 , \bhb_3 )\) relative to basis \((\be_1 , \be_2 , \be_3 )\text{:}\) this would allow for the determination of position vector \(\br_{BP}\) if \(P\) is at a specified location relative to \(B\text{.}\)
The position of \(B\) in \(\cB\) is defined by adopting a coordinate system (Section 1.2). The orientation of \(\cB\) can be defined in three possible ways:
- (ii) by one of twelve possible Euler sequences (Section 1.4) , and
- (iii) by a single equivalent rotation (Section 1.5) represented in terms of an angle and a direction or in terms of a quaternion (Section 1.6).