Skip to main content

Advanced Engineering Dynamics

R. Valéry Roy

Section 3.2 Practical Determination of Angular Velocity

A practical way of determining angular velocities is to introduce a sequence of auxiliary referentials \(\cA_{1}\text{,}\) \(\cA_{2}\text{,}\) \(\ldots\text{,}\) \(\cA_{n-1}\) so that a basis \(b_{\cA}\) of \(\cA\) is mapped onto a basis \(b_\cB\) of \(\cB\) by a sequence of rotations
\begin{equation*} b_\cA \xrightarrow{\cR_1} b_{\cA_1}\xrightarrow{\cR_2} \ldots b_{\cA_{n-1}} \xrightarrow{\cR_n} b_\cB \end{equation*}
If such a sequence can be found, and if each angular velocity \(\bom_{\cA_{k+1}/\cA_k}\) can be determined, then the angular velocity \(\bom_{\cB/ \cA}\) can be found by using the following result.

Proof.

Given an arbitrary vector \(\bvv\text{,}\) we have according to (3.1.3)
\begin{equation*} \left( {d \bvv \over dt } \right)_{\cA} = \left( {d \bvv \over dt } \right)_{\cB} + \bom_{\cB/ \cA} \times \bvv \end{equation*}
\begin{equation*} \left( {d \bvv \over dt } \right)_{\cC} = \left( {d \bvv \over dt } \right)_{\cA} + \bom_{\cA/ \cC} \times \bvv \end{equation*}
\begin{equation*} \left( {d \bvv \over dt } \right)_{\cB} = \left( {d \bvv \over dt } \right)_{\cC} + \bom_{\cC/ \cB} \times \bvv \end{equation*}
Then, by summing these equations, we find \(( \bom_{\cB/ \cA}+\bom_{\cA/ \cC}+\bom_{\cC/ \cB} ) \times \bvv = \bze\) for all vectors \(\bvv\text{.}\) Hence \(\bom_{\cB/ \cA}+\bom_{\cA/ \cC}+\bom_{\cC/ \cB}= \bze\text{.}\) First let \(\cC\) coincide with \(\cA\text{:}\) we obtain the identity \(\bom_{\cB/ \cA}= - \bom_{\cA/ \cB}\) given that \(\bom_{\cA/ \cA}={\bf 0}\text{.}\)
As a consequence of (3.2.1) we have two simple identities:
\begin{equation} \bom_{\cB/ \cA} = - \bom_{\cA / \cB}\tag{3.2.2} \end{equation}
and
\begin{equation} \bom_{\cA/ \cA} = \bze\tag{3.2.3} \end{equation}
The simplest orientation between two referentials \(\cA\) and \(\cB\) is modeled as a planar rotation, that is, a rotation about a common axis: assume that the basis \(b_A\) of \(\cA\) can be mapped onto basis \(b_B\) of \(\cB\) by the rotation \(\cR_{\theta ,\bha_3}\) of angle \(\theta\) about unit vector \(\bha_3 = \bhb_3\) fixed in both \(\cA\) and \(\cB\text{:}\)
\begin{equation*} (\bha_1 , \bha_2, \bha_3) \xrightarrow{\cR_{\theta , \, \bha_3}} (\bhb_1 , \bhb_2, \bhb_3= \bha_3) \end{equation*}
The orientation of \(\cB\) relative to \(\cA\) is then characterized by the oriented angle \(\theta = (\bha_1 , \bhb_1) = (\bha_2 , \bhb_2)\text{.}\) By convention, the positive sense of rotation about vector \(\bha_3\) is given by the right-hand-rule. See Figure 3.2.2. Then, the angular velocity of \(\cB\) relative to \(\cB\) is given by
\begin{equation} \bom_{\cB / \cA} = \dot{\te} \bha_3\tag{3.2.4} \end{equation}
Indeed, it is easy to show that \((d\bhb_1 /dt)_\cA = \dte \bhb_2 = \dte \bha_3 \times \bhb_1\) and \((d\bhb_2 /dt)_\cA =- \dte \bhb_1 = \dte \bha_3 \times \bhb_2\text{.}\)
Figure 3.2.2. Simple rotation
Now consider an arbitrary rotation between \(\cA\) and \(\cB\text{.}\) A basis of \(\cA\) can be mapped to a basis of \(\cB\) by \(n\) consecutive planar rotations of angle \(\te_{i}\) about unit vector \(\bk_{i}\text{,}\) each rotation defining an auxiliary referential \(\cA_{i}\text{:}\)
\begin{equation} b_{\cA_0}= b_\cA \xrightarrow{\cR_{\theta_1 , \bk_1}} b_{\cA_1} \xrightarrow{\cR_{\theta_2 , \bk_2}} b_{\cA_2} \rightarrow\cdots\rightarrow b_{\cA_{n-1}} \xrightarrow{\cR_{\theta_{n} , \bk_{n}}} b_{\cA_{n}}= b_\cB\tag{3.2.5} \end{equation}
where unit vector \(\bk_i\) is fixed in both \(\cA_{i-1}\) and \(\cA_{i}\text{.}\) Then, according to (3.2.1), we have
\begin{equation} \bom_{\cB/ \cA} = \dot{\te}_{1} \; \bk_{1} + \dot{\te}_{2} \; \bk_{2} + \cdots +\dot{\te}_{n} \; \bk_{n} \tag{3.2.6} \end{equation}

Remark 3.2.3.

The determination of \(\bom_{\cB / \cA}\) is intimately related to the parametrization of the orientation of \(\cB\) relative to \(\cA\text{.}\) In particular, Euler sequences introduced in Section 1.4 is a particular case of sequence (3.2.5).

Remark 3.2.4.

A representation of \(\bom_{\cB/ \cA}\) such as (3.2.6) yields an expression which is generally resolved neither on a basis of \(\cA\) nor on a basis of \(\cB\text{.}\)
The remainder of this section demonstrates through examples the efficiency of formula (3.1.3) for the determination of time-derivatives of vectors by the use of angular velocities.

Example 3.2.5.

A point \(P\) is in motion in a referential \(\cE\) of Cartesian axes \(Oxyz\text{.}\) Its position is defined by the spherical coordinates \((\ro, \phi, \te)\) as defined in Subsection 1.2.3.
Find the velocity \(\vel_{P/\cE}\) of \(P\) relative to \(\cE\) by defining a fictitious referential \(\cF\) relative to which the unit vectors \((\be_\ro, \be_\phi , \be_\te )\) are attached. See Figure 3.2.6.
Figure 3.2.6. Spherical coordinates
Solution.
To the spherical coordinates \((\ro, \phi, \te)\) of a point \(P\) corresponds the moving basis of unit vectors \((\be_\ro , \be_\phi , \be_\te )\text{.}\) The velocity of point \(P\) is obtained by differentiating the position vector \(\br_{OP} = \ro \,\be_\ro\) relative to \(\cE\text{:}\)
\begin{equation*} \vel_{P/\cE} = \dro \,\be_\ro + \ro \left({d\be_\ro \over dt} \right)_\cE. \end{equation*}
Hence, we need to find the derivative of \(\be_\ro\text{:}\) according to (3.1.3) we have
\begin{equation*} \left({ d\be_\ro \over dt} \right)_\cE = \bom_{\cF / \cE} \times \be_\ro \end{equation*}
where \(\cF\) denotes a fictitious referential relative to which basis \((\be_\ro , \be_\phi , \be_\te )\) is fixed. The angular velocity \(\bom_{\cF / \cE}\) is found by two consecutive planar rotations:
  • the rotation of angle \(\te\) about \(\be_z\) maps basis \((\be_x , \be_y , \be_z )\) to basis \((\be_r , \be_\te , \be_z )\) of an auxiliary referential \(\cE_1\text{.}\)
  • the rotation of angle \(\phi\) about \(\be_\te\) maps basis \((\be_r , \be_\te , \be_z )\) to basis \((\be_\phi , \be_\te , \be_\ro )\) of referential \(\cF\text{.}\)
\begin{equation*} (\be_x , \be_y , \be_z) \xrightarrow{\cR_{\te , \, \be_z}} (\be_r , \be_\te , \be_z) \xrightarrow{\cR_{\phi , \, \be_\te}} (\be_\phi , \be_\te , \be_\ro) \end{equation*}
These transformations are summarized in the following rotation diagrams:
Figure 3.2.7. Rotation diagrams
We can now write
\begin{equation*} \bom_{\cF/ \cE} = \bom_{\cF/ \cE_{1}} + \bom_{\cE_{1} / \cE} = \dphi \,\be_\te + \dte \be_z \end{equation*}
The velocity of \(P\) can then be found as the straightforward determination of cross-products
\begin{align*} \vel_{P/\cE} \amp = \dro \,\be_\ro + \ro \bom_{\cF / \cE} \times \be_\ro = \dro \,\be_\ro + \ro \,(\dphi \,\be_\te + \dte \be_z)\times \be_\ro\\ \amp = \dro \,\be_\ro + \ro \,(\dphi \,\be_\phi + \dte \sin\phi \,\be_\theta ) \end{align*}
where we have determined the cross-products \(\be_\te \times \be_\ro\) and \(\be_z\times \be_\ro\) by direct inspection of the rotation diagrams: \(\be_\te \times \be_\ro =\be_\phi \text{,}\) \(\be_z\times \be_\ro = \sin\phi \,\be_\theta\text{.}\)
In order to find the acceleration of \(P\text{,}\) one would need the derivative of unit vector \(\be_\phi\text{.}\) It is found in the following way:
\begin{equation*} \left( {d \be_\phi \over dt } \right)_\cE = \bom_{\cF / \cE} \times \be_\phi = (\dphi \,\be_\te + \dte \be_z ) \times \be_\phi = - \dphi \,\be_\ro + \dte \cos\phi \,\be_\te \end{equation*}

Remark 3.2.8.

We could have found \(\vel_{P/\cE}\) by using formula (3.1.3) between \(\cE\) and \(\cF\) applied to \(\bvv = \br_{OP}\text{:}\)
\begin{equation*} \vel_{P/\cE} = \left( {d \over dt } (\ro \be_\ro) \right)_{\cF} + \bom_{\cF/ \cE} \times \ro \be_\ro \end{equation*}
The same result is found.

Remark 3.2.9.

To fully appreciate the efficiency of this approach, compare it with the method which would consist of first resolving \(\be_\ro\) on basis \((\be_x , \be_y , \be_z)\text{,}\) then differentiating each component, and finally expressing the final answer on basis \((\be_\phi , \be_\te , \be_\ro)\text{.}\)

Example 3.2.10.

Determine the angular velocity \(\bom_{\cB / \cE}\) of the referential \(\cB\) whose orientation is parametrized in terms of Euler angles \((\psi , \te , \phi )\) shown in Figure 3.2.11. Express \((\dpsi , \dte , \dphi)\) in terms of the components \((p,q,r)\) of \(\bom_{\cB / \cA}\) on basis \((\bhb_1 , \bhb_2 , \bhb_3 )\text{.}\) Then find the derivatives of \(\bhb_i\) (\(i=1,2,3\)). relative to referential \(\cE\text{.}\)
Figure 3.2.11. Euler angles
Solution.
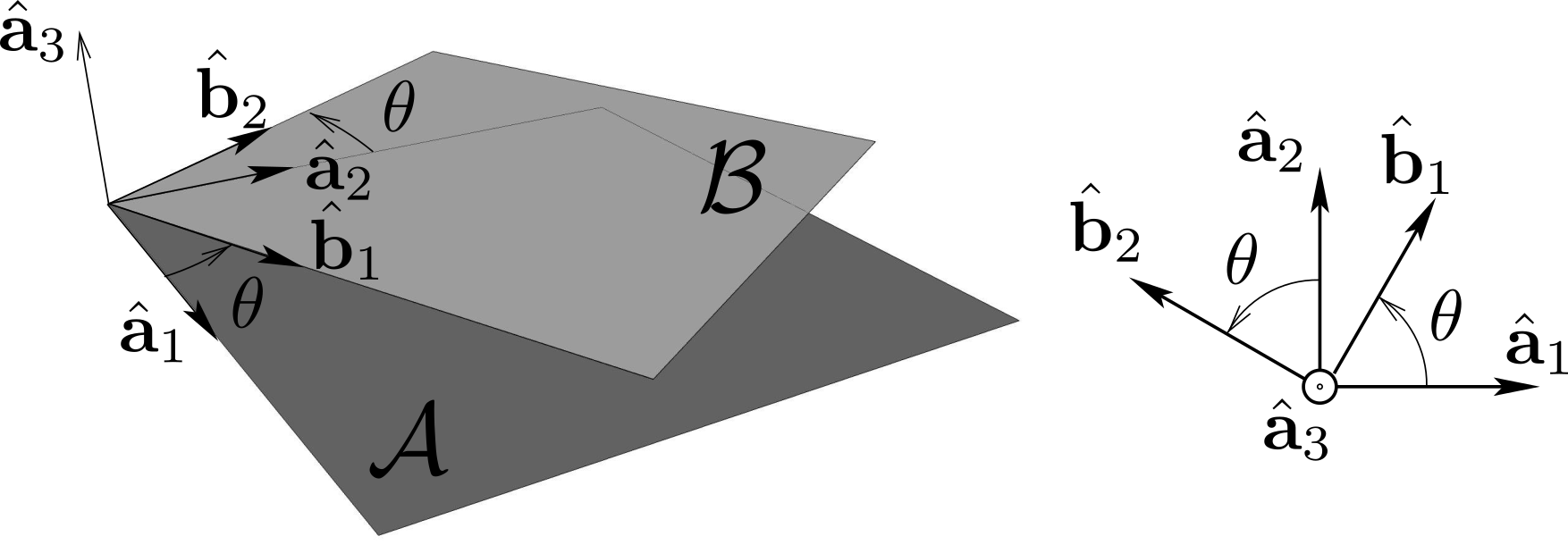
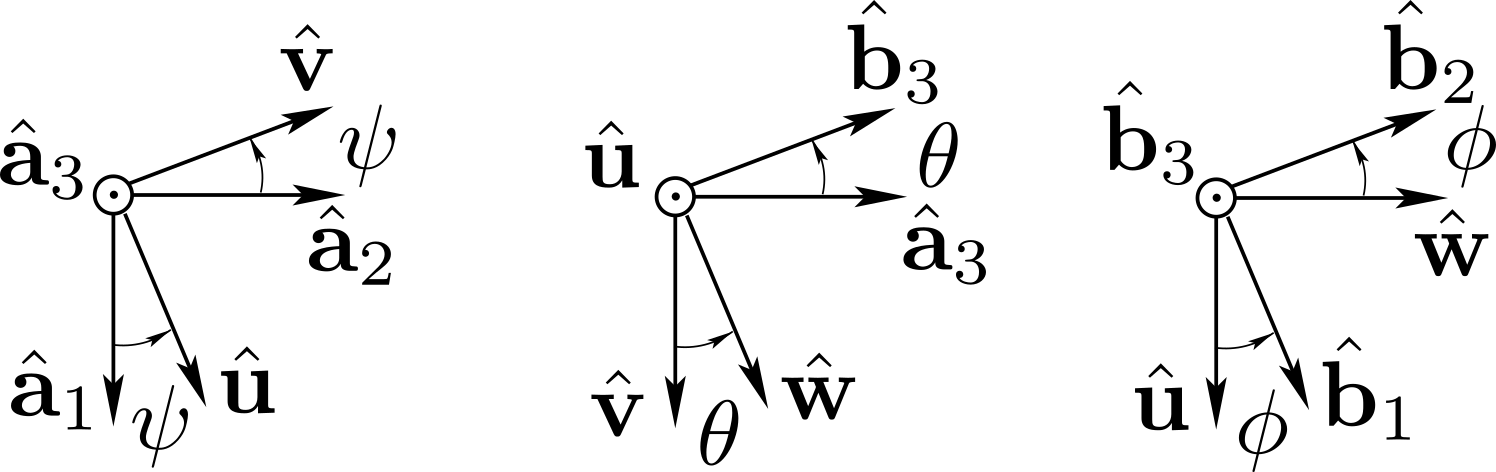
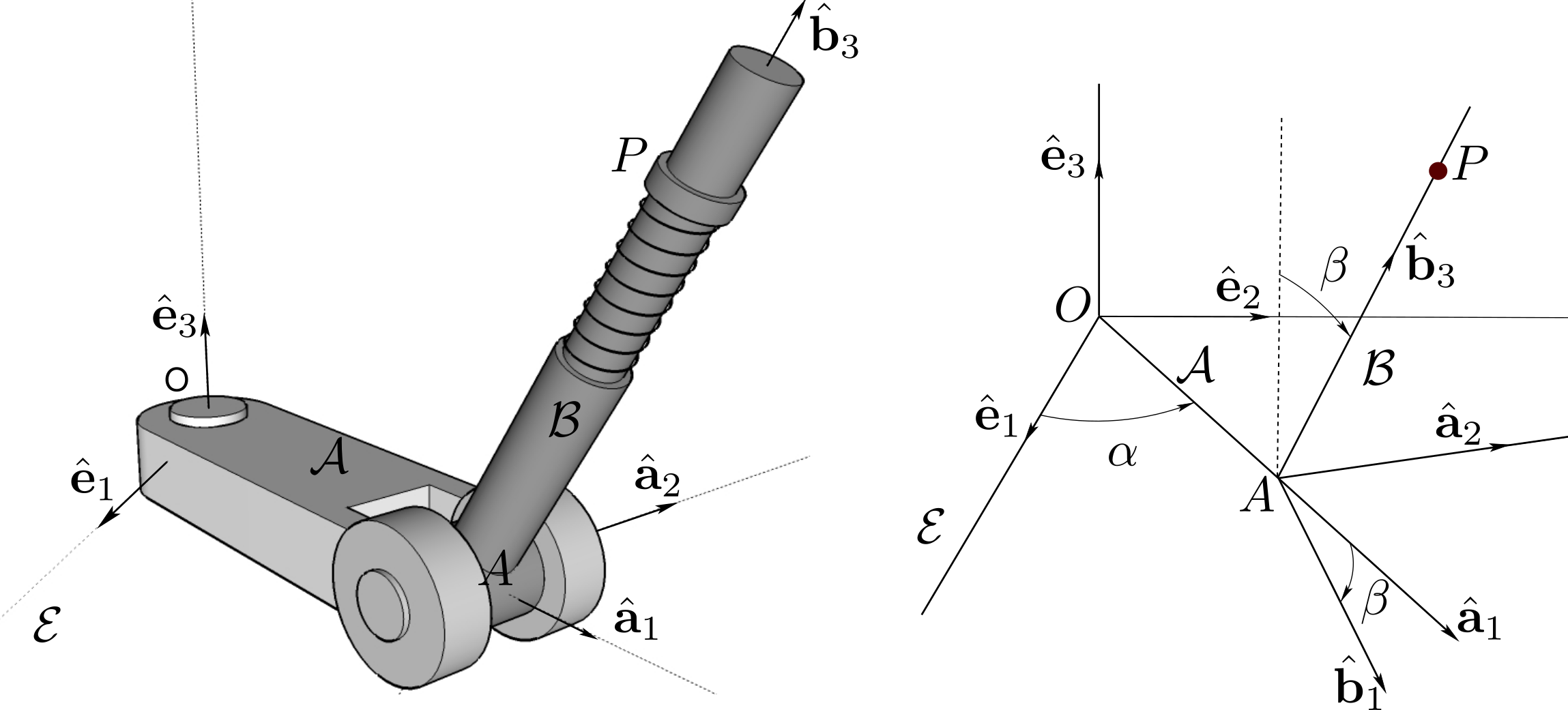
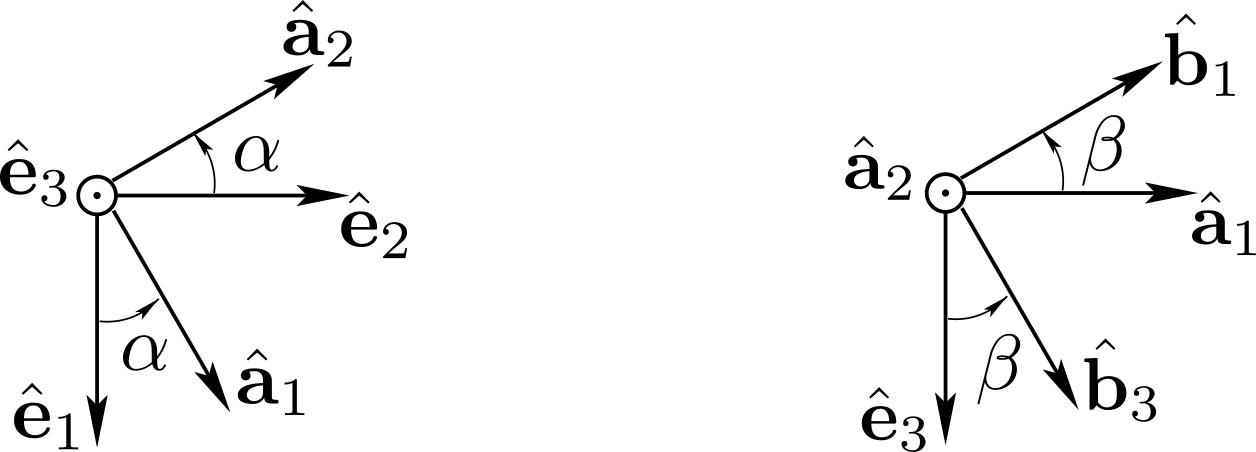The sequence of transformations which maps basis \((\be_1 , \be_2 , \be_3 )\) of \(\cE\) into basis \((\bhb_1 , \bhb_2 , \bhb_3 )\) of \(\cB\) leads to
\begin{equation*} \bom_{\cB / \cE} =\dpsi \be_3 + \dte \bu_1 + \dphi \bhb_3 \end{equation*}
We can resolve \(\bom_{\cB / \cE}\) on basis \((\bhb_1 , \bhb_2 , \bhb_3 )\) to obtain \((p,q,r)\)
\begin{align*} p \amp = \dpsi \sin\te\sin\phi + \dte \cos\phi \\ q \amp = \dpsi \sin\te\cos\phi - \dte \sin\phi \\ r \amp = \dpsi \cos\te + \dphi \end{align*}
We can then express \((\dpsi, \dte, \dphi)\) in terms of \((p,q,r)\)
\begin{align*} \dpsi \amp = (p \sin\phi + q \cos\phi)/ \sin\te \\ \dte \amp = {p \cos\phi - q \sin\phi} \\ \dphi \amp = r - \cot\te (p \sin\phi + q \cos\phi) \end{align*}
To differentiate \(\bhb_1\text{,}\) we apply formula (3.1.3) (recall that \(\bhb_1\) is attached to \(\cB\text{.}\)
\begin{align*} \left( {d \bhb_1 \over dt } \right)_{\cE} \amp = \left( {d \bhb_1 \over dt } \right)_{\cB} + \bom_{\cB/ \cE} \times \bhb_1 = ( \dpsi \be_3 + \dte \bu_1 + \dphi \bhb_3 ) \times \bhb_1 \\ = \amp \dpsi (\cos\te \bhb_2 -\sin\te\cos\phi \bhb_3) + \dte \sin\phi \bhb_3 + \dphi \bhb_2 \end{align*}
where we have found the following cross-products from the rotation diagrams displayed above
\begin{equation*} \be_3 \times \bhb_1 = \cos\te \bhb_2 -\sin\te \cos\phi \bhb_3, \quad \bu_1 \times \bhb_1 = \sin\phi \bhb_3, \quad \bhb_3 \times \bhb_1 = \bhb_2 \end{equation*}
Regroup likewise terms to obtain
\begin{equation*} \left( {d \bhb_1 \over dt } \right)_{\cE} = (\dpsi \cos\te + \dphi) \bhb_2 + (\dte \sin\phi - \dpsi \sin\te\cos\phi) \bhb_3 \end{equation*}
Note that since \(\bhb_1\) is a unit vector, its derivative is normal to itself. The reader will verify the following results
\begin{equation*} \left( {d \bhb_2 \over dt } \right)_{\cE} = - (\dpsi \cos\te + \dphi) \bhb_1 + (\dte \cos\phi + \dpsi \sin\te\sin\phi) \bhb_3 \end{equation*}
(which can be found from the derivative of \(\bhb_1\) by changing \(\phi\) to \(\phi + \pi/2\)),
\begin{equation*} \left( {d \bhb_3 \over dt } \right)_{\cE} = \dpsi \sin\te \bu_1 + \dte \bv_2 \end{equation*}
Note the singularity at \(\te =0\) and \(\te= \pi\) in the expression \(\dpsi = (p \sin\phi + q \cos\phi)/\sin\te\text{,}\) consistent with the indetermination of Euler angles described in Section 1.4.

Example 3.2.12.

Two rigid bodies \(\cA\) and \(\cB\) are in motion in a referential \(\cE\) of origin \(O\) and basis \((\be_1 , \be_2 , \be_3 )\text{.}\) Body \(\cA (O, \bha_1 , \bha_2 , \bha_3 )\) is in rotation about axis \((O, \be_3 )\) of \(\cE\text{.}\) Its orientation is parametrized by angle \(\alpha = (\be_1 , \bha_1)\text{.}\) Denote by \(A\) the point of \(\cA\) defined by \(\br_{OA} = a \bha_1 \text{.}\) Body \(\cB (A, \bhb_1 , \bhb_2 , \bhb_3)\) rotates relative to \(\cA\) about axis \((A, \bha_2)\text{.}\) Its orientation is parametrized by angle \(\beta = (\bha_1 , \bhb_1)\text{.}\) Finally, a collar \(P\) slides along body \(\cB\text{:}\) its position is defined by \(\br_{AP} = \ro (t) \bhb_3\text{.}\) See Figure 3.2.13.
  1. Find the time-derivative of unit vectors \(\bhb_1\) and \(\bhb_3\) relative to \(\cE\text{.}\)
  2. Find the velocity of \(P\) in referential \(\cE\) in terms of \(\rho\text{,}\) \(\alpha\text{,}\) \(\beta\) and their time-derivatives.
Figure 3.2.13.
Solution.
  1. We have the following transformations between referentials \(\cE\text{,}\) \(\cA\) and \(\cB\text{:}\)
    \begin{equation*} (\be_1 , \be_2 , \be_3) \xrightarrow{\cR_{\al , \, \be_3}} (\bha_1 , \bha_2 , \bha_3=\be_3)\xrightarrow{\cR_{\beta , \, \bha_2 }} (\bhb_1 ,\bhb_2 = \bha_2 , \bhb_3) \end{equation*}
    and we can sketch the corresponding rotation diagrams
    Figure 3.2.14.
    leading to the corresponding angular velocities \(\bom_{\cA / \cE}= \dot{\al} \be_3\text{,}\) \(\bom_{ \cB / \cA} = \dot{\beta} \bha_2\text{,}\) and \(\bom_{ \cB / \cE} = \dot{\al} \be_3+ \dot{\beta} \bha_2\text{.}\) We can now find \((d\bhb_1 /dt)_{\cE}\) and \((d\bhb_3 /dt)_{\cE}\text{:}\)
    \begin{equation*} \left( {d\bhb_1 \over dt } \right)_{\cE} = \bom_{ \cB / \cE} \times \bhb_1 = \dal \cos\beta \bha_2 - \dbe \bhb_3 \end{equation*}
    \begin{equation*} \left( {d\bhb_3 \over dt } \right)_{\cE} = \bom_{ \cB / \cE} \times \bhb_3 = \dal \sin\beta \bha_2 + \dbe \bhb_1 \end{equation*}
    where the cross-products \(\be_3 \times \bhb_3\text{,}\) \(\be_3 \times \bhb_1\) and \(\bha_2 \times \bhb_3\) are determined directly from the rotation diagrams.
  2. The velocity of particle \(P\) in \(\cE\) is obtained by differentiating (relative to \(\cE\)) the position vector \(\br_{OP} = a \bha_1 + \ro \bhb_3\) one term at a time:
    \begin{align*} \vel_{P/\cE} \amp = a \left( {d\bha_1 \over dt } \right)_{\cE} + \dro \, \bhb_3 + \ro \left( {d\bhb_3 \over dt } \right)_{\cE}\\ \amp = a \dal \, \bha_2 + \dro \, \bhb_3 + \ro (\dal \sin\beta \, \bha_2 + \dbe \, \bhb_1)\\ \amp = (a \dal + \ro \dal \sin\beta) \bha_2 +\dro \, \bhb_3 + \ro\dbe \, \bhb_1 \end{align*}
The mistake to avoid here is to write \(\vel_{P/\cE} = \bom_{\cB/\cE} \times \br_{OP}\text{.}\) This is incorrect since \(\br_{OP}\) is not fixed to referential \(\cB\text{.}\) However, we could write
\begin{equation*} \vel_{P/\cE}= (d\br_{OP} /dt)_\cB + \bom_{\cB/\cE} \times \br_{OG} \end{equation*}
but this is not practical since \(\br_{OP}\) varies relative to both \(\cE\) and \(\cB\text{.}\)

Example 3.2.15.

A gyroscopic system consists of three interconnected rigid bodies \(\cA\text{,}\) \(\cB\text{,}\) and \(\cC\) in motion in a referential \(\cE (O, \be_1, \be_2 , \be_3)\text{.}\) The outer gimbal \(\cA (O, \bha_{1},\bha_{2},\bha_{3}= \be_3)\) is in rotation relative to referential \(\cE\) about fixed axis \((O, \be_3)\text{.}\) Connected to \(\cA\) is the inner gimbal \(\cB (O, \bhb_{1} = \bha_1 ,\bhb_{2} , \bhb_{3})\) which is free to rotate relative to \(\cA\) about axis \((O, \bha_1)\text{.}\) Finally rotor \(\cC (O, \bhc_{1} ,\bhc_{2} = \bhb_2,\bhc_{3})\) can rotate relative to \(\cB\) about axis \((O, \bhb_2)\text{.}\) The rotation diagrams mapping basis \((\be_1, \be_2 , \be_3)\) to basis \((\bhc_{1} ,\bhc_{2},\bhc_{3})\) are shown in Figure 3.2.16.
  1. Find the time derivative of each vector of basis \((\bhc_{1} ,\bhc_{2},\bhc_{3})\) relative to \(\cE\text{.}\)
  2. Deduce the velocity of point \(P\) of \(\cC\) defined by \(\br_{OP}= R \bhc_1\) (\(R \) is a constant).
Figure 3.2.16.
Solution.
  1. Each of the motions \(\cA /\cE\text{,}\) \(\cB/\cA\text{,}\) and \(\cC /\cB\) is a planar rotation. The corresponding angular velocities are then easily found from the diagrams showing the configurations of the bases of \(\cE\text{,}\) \(\cA\text{,}\) \(\cB\) and \(\cC\text{:}\) \(\bom_{\cA / \cE }= \dot{\al} \be_{3}\text{,}\) \(\bom_{\cB / \cA} = \dot{\beta} \bha_{1}\) and \(\bom_{\cC / \cB}= \dot{\ga} \bhb_{2}\text{.}\) Hence we have
    \begin{equation*} \bom_{\cC /\cE}= \dot{\al} \be_{3}+\dot{\beta} \bha_{1}+\dot{\ga} \bhb_{2}. \end{equation*}
    We find the time derivative of \(\bhc_1\) by using \(\bom_{\cC / \cE} \times \bhc_{1}\text{:}\)
    \begin{align*} \left( {d\bhc_2 \over dt } \right)_{\cE} \amp = (\dot{\al} \be_{3}+\dot{\beta} \bha_{1}+\dot{\ga} \bhb_{2})\times \bhc_{1} = \dot{\al} \be_{3}\times \bhc_{1} + \dot{\beta} \bha_{1}\times\bhc_{1} - \dot{\ga} \bhc_{3} \\ \amp = \dot{\al}( \cos\beta\cos\ga\bhc_{2} -\sin\beta\bhc_{3}) + \dot{\beta} \sin\ga \bhc_{2} - \dot{\ga} \bhc_{3} \\ \amp = (\dot{\beta} \sin\ga + \dot{\al}\cos\beta\cos\ga)\bhc_{2} - (\dot{\ga}+\dot{\al}\sin\beta)\bhc_{3} \end{align*}
    Note that, as expected, \(( {d\bhc_{1} / dt } )_{\cE}\) is orthogonal to \(\bhc_{1}\text{.}\) Likewise, the derivatives \(( {d\bhc_{2} / dt } )_{\cE}\) and \(( {d\bhc_{3} / dt } )_{\cE}\) are found to be given by:
    \begin{equation*} \left( {d\bhc_2 \over dt } \right)_{\cE} = \bom_{\cB / \cE} \times \bhc_2 = - \dal\cos\beta \, \bhb_1 + \dbe \, \bhb_3 \end{equation*}
    \begin{align*} \left( {d\bhc_3 \over dt } \right)_{\cE} = \bom_{\cC / \cE} \times \bhc_3 = (\dot{\al}\sin\beta- \amp \dot{\beta} \sin\ga +\dot{\ga})\bhc_{1} \\ \amp +(\dot{\al}\cos\beta\sin\ga +\dot{\beta}\cos\ga )\bhc_{2} \end{align*}
  2. Velocity \(\vel_{P/\cE}\) is found by time-differentiating position vector \(\br_{OP} = R \bhc_1\) relative to \(\cE\text{.}\) Since \(R\) is a constant, we find
    \begin{equation*} \vel_{P/\cE} =R (\dot{\beta} \sin\ga + \dot{\al}\cos\beta\cos\ga)\bhc_{2} - R(\dot{\ga}+\dot{\al}\sin\beta)\bhc_{3} \end{equation*}
PrevTopNext