Skip to main content

Advanced Engineering Dynamics

R. Valéry Roy

Section 13.7 Painlevé Equation

Consider a rigid body \(\cB\) whose position relative to a Newtonian referential \(\cE\) is defined by the \((n+1)\) independent coordinates \((q_1, q_2, \ldots q_n, t)\text{.}\) Assume that the variables \((\bq,t)\) are independent. The kinetic energy can be viewed in general as a quadratic form in the variables \((\dq_1, \dq_2,\ldots, \dq_n)\text{.}\) This can be shown as follows:
\begin{align*} \vel_{P/\cE} ^2 \amp = \big(\frac{d\br}{dt}\big)^2 = \big( \dq_1 \frac{\partial\br}{\partial q_1} +\cdots+ \dq_n \frac{\partial\br}{\partial q_n}+ \frac{\partial\br}{\partial t} \big)^2\\ \amp = \dq_i \dq_j \frac{\partial\br}{\partial q_i}\cdot \frac{\partial\br}{\partial q_j} + \dq_i \frac{\partial\br}{\partial q_i}\cdot \frac{\partial\br}{\partial t} + \big(\frac{\partial\br}{\partial t})^2 \end{align*}
denoting \(\br= \br_{OP}\) and using the summation convention for repeated indices. This leads to the following decomposition:

Remark 13.7.2.

\(\kin^{(k)}_{\cB/\cE}\) is of degree \(k\) in the variables \(\dq_i\text{.}\)

Remark 13.7.3.

In practice, the \(k\)th-order contribution of the kinetic energy is found by first determining the expression \(\kin_{\cB/\cE}\) (making sure that \(q_1, q_2, \ldots q_n, t\) are treated as independent variables) and collecting all term in \(\dq_i\) of order \(k\) in this expression.
Painlevé equation can be found by following the now familiar approach: we choose the following virtual velocity field
\begin{equation*} \vel_P^* = \dq_1 \frac{\partial\br}{\partial q_1} +\cdots+ \dq_n \frac{\partial\br}{\partial q_n} +\frac{\partial\br}{\partial t} \end{equation*}
assuming that the variables \((q_1, \ldots q_n,\dq_1, \ldots, \dq_n, t)\) are independent. This field defines a screw since it is a linear combinations of screws. We then apply the Principle of Virtual Power: this leads to the determination of two virtual power terms:
  • the virtual power of inertial forces \(\int_\cB \vel_P^* \cdot (-\ba_P) dm\text{,}\)
  • the virtual powers of external body forces \(\int_\cB \vel_P^* \cdot \bF_P dV\) and contact forces \(\int_{\partial\cB} \vel_Q^* \cdot \bof_Q dA\text{.}\) These terms involve the power coefficients \(\qQ^{q_i}_{\coB\to \cB/\cE}\) of the external actions:
    \begin{equation} \sum_{i=1}^n \dq_i \qQ^{q_i}_{\coB\to \cB/\cE}\tag{13.7.1} \end{equation}
To find the virtual power of inertial forces, we must find an expression of the \(\vel_P^* \cdot \ba_P\text{:}\)
\begin{align*} \vel_P^* \cdot \ba_P \amp = \dq_i \frac{\partial\br}{\partial q_i} \cdot \frac{d}{dt}\left( \dq_j \frac{\partial\br}{\partial q_j} + \frac{\partial\br}{\partial t} \right)\\ \amp = \dq_i \frac{\partial\br}{\partial q_i} \cdot \frac{d}{dt}\left( \dq_j \frac{\partial\br}{\partial q_j} \right) + \dq_i \frac{\partial\br}{\partial q_i} \cdot \frac{d}{dt}\left(\frac{\partial\br}{\partial t} \right)\\\\ \amp = \underbrace{\frac{d}{dt}\left( \half \dq_i \dq_j \frac{\partial\br}{\partial q_i} \frac{\partial\br}{\partial q_j} \right)}_ {\text{term #1}} + \underbrace{\dq_i \frac{\partial\br}{\partial q_i} \cdot \frac{d}{dt}\left(\frac{\partial\br}{\partial t} \right)}_ {\text{term #2}} \end{align*}
Upon integrating over the volume of body \(\cB\text{,}\) three kinetic energy terms are obtained:
  1. in the term #1 we recognize the kinetic energy of order 2: it leads to \(\frac{d}{dt}\kin^{(2)}_{\cB/\cE}\)
  2. term #2 is transformed as follows:
    \begin{align*} \dq_i \frac{\partial\br}{\partial q_i} \cdot \frac{d}{dt}\left(\frac{\partial\br}{\partial t} \right) \amp = \left(\vel_P - \frac{\partial\br}{\partial t} \right) \cdot \frac{d}{dt}\left(\frac{\partial\br}{\partial t} \right)\\ \amp = \underbrace{\vel_P\cdot \frac{d}{dt}\left(\frac{\partial\br}{\partial t}\right)}_ {\text{term #2.1}} - \underbrace{\frac{d}{dt}\left(\half \frac{\partial\br}{\partial t} \cdot\frac{\partial\br}{\partial t} \right)}_ {\text{term #2.2}} \end{align*}
    The term #2.1 can be written as follows
    \begin{equation*} \vel_P \cdot \big( \dq_i \frac{\partial^2\br}{\partial q_i\partial t} + \frac{\partial^2\br}{\partial t^2} \big) = \vel_P \cdot \frac{\partial}{\partial t} \vel_P = \frac{\partial}{\partial t} (\half \vel_P^2 ) \end{equation*}
    and its integration over \(\cB\) leads to \(\frac{\partial}{\partial t}\kin_{\cB/\cE}\text{.}\) Finally, the integration of term #2.2 leads to \(\frac{d}{dt}\kin^{(0)}_{\cB/\cE} \text{.}\)
By collecting all the terms we arrive at Painlevé equation:
It is possible to generalize Painlevé equation (13.7.2) to a system \(\Si\) of \(p\) rigid bodies
\begin{equation} \frac{d}{dt}(\kin^{(2)}_{\Si/\cE} -\kin^{(0)}_{\Si/\cE} )+ \frac{\partial}{\partial t}\kin_{\Si/\cE} = \sum_{i=1}^n \dq_i \qQ^{q_i}_{\bSi\to \Si/\cE} + \sum_{i=1}^n\sum_{1\leq k \lt l\leq p} \dq_i \qQ^{q_i}_{k \leftrightarrow l}\tag{13.7.3} \end{equation}
An interesting corollary follows from Painlevé equation:

Proof.

The proof stems from the assumptions (i)-(iii): all power coefficients \(\qQ^{q_i}_{\bSi\to \Si/\cE}\) and \(\qQ^{q_i}_{k \leftrightarrow l}\) are either zero by assumption (i) or can be expressed in the form \(-\partial \pot/\partial q_i\text{.}\) With \(\partial\kin_{\Si/\cE} /\partial t =0\) and \(\partial\pot /\partial t =0\) we obtain (13.7.4).
The following problem illustrates the use of Painlevé equation.

Example 13.7.6.

We consider the motion of a system \(\Sigma\) relative to a Newtonian referential 0\((O, \bx_0, \by_0, \bz_0 )\text{.}\) Axis \((O,\bz_0)\) is directed upward (\({\bf g}=-g\bz_0\)). The system \(\Sigma\) is comprised of two rigid bodies 1 and 2 described as follows:
Body 1\((O, \bx_1,\by_1,\bz_0)\) is a torus-shaped body, of homogeneous density, mass center \(O\text{,}\) radius \(R\text{,}\) and mass \(m_1\text{.}\) The plane \((O, \bx_1, \bz_1)\) is a plane of symmetry. Body 1 is connected to referential 0 by an ideal pivot of axis \((O,\bz_0)\text{,}\) and its position is defined by angle \(\psi = (\bx_0,\bx_1)= (\by_0 ,\by_1)\text{.}\) Denote by \(I_1\) the moment of inertia of body 1 about axis \((O,\bz_0)\text{.}\)
Figure 13.7.7.
Body 2\((G,\bx_2 ,\by_2 = \by_1 ,\bz_2)\) is a truncated toroidal shell of mass \(m_2\) and mass center \(G\) with \(\br_{OG}= R \bx_2\text{.}\) The exterior surface of body 1 is in contact with the interior surface of body 2: body 2 is free to “slide” relative to body 1, and its motion relative to 1 is parametrized by angle \(\theta = (\bx_1 , \bx_2) = (\bz_0, \bz_2)\text{.}\) Its inertia operator about \(G\) is represented by:
\begin{equation*} [\cI_{G, 2}]_{b_2} = \begin{bmatrix} A_2 \amp 0 \amp 0 \\ 0 \amp B_2 \amp 0 \\ 0 \amp 0 \amp C_2 \end{bmatrix}_{b_2} \end{equation*}
on basis \(b_2 (\bx_2,\by_2,\bz_2)\text{.}\)
The joint between 1 and 2 is assumed ideal. A motor \(\cal M\) is mounted between 0 and 1, and imposes a prescribed angle \(\psi (t)= \Om t\) where \(\Om\) is a positive constant. The action of \(\cM\) on 1 is equivalent to a couple \(\cC \bz_0\text{.}\)
  1. Determine Painlevé equation applied to system \(\Sigma\text{.}\) Does it lead to a first integral?
  2. Determine Lagrange equations applied to system \(\Sigma\) w.r.t. \(q=\psi,\te\text{.}\) Recover the results of a).
Solution.
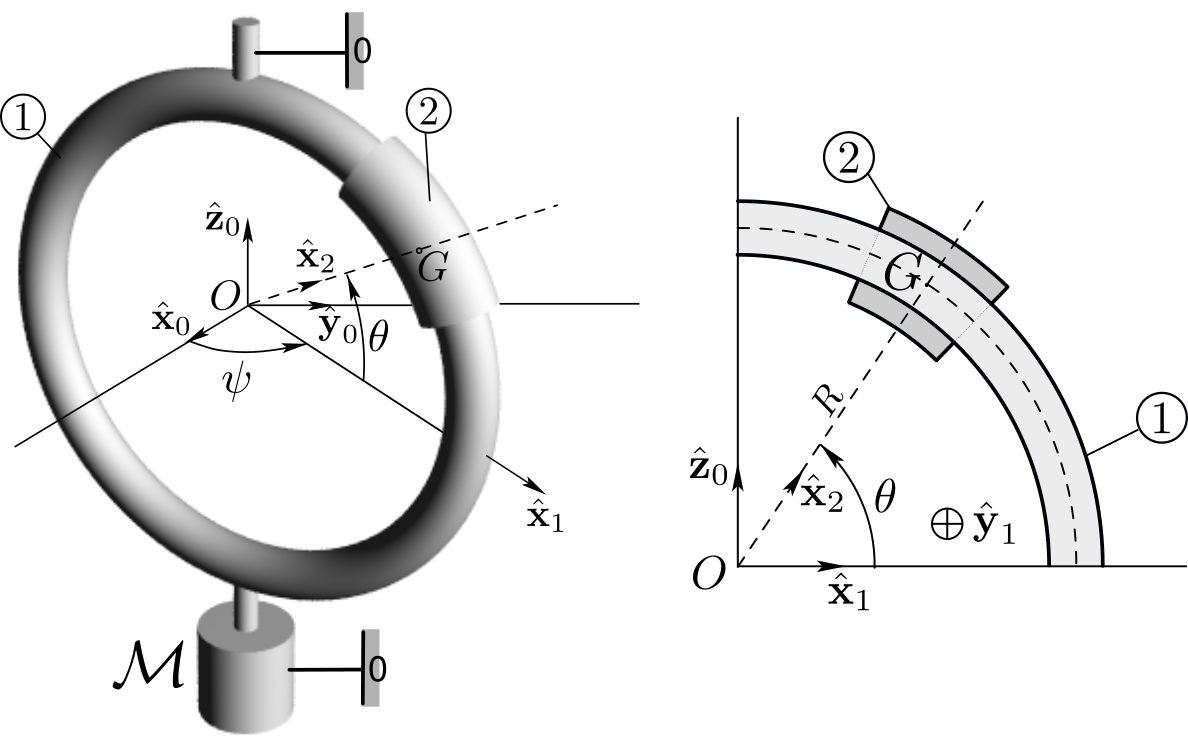
a. The position of system \(\Si\) is parametrized by angle \(\theta\) and time \(t\text{.}\) The kinematic screws of bodies 1 and 2 are written as
\begin{equation*} \{ \cV_{1/0} \} = \{ \cV^t_{1/0} \} = \begin{Bmatrix} \Om\bz_0\\\\ \bze \end{Bmatrix}_O, \end{equation*}
\begin{equation*} \{ \cV_{2/0} \} = \dte \{ \cV^\te_{2/0} \} + \{ \cV^t_{2/0} \} = \dte \begin{Bmatrix} -\by_1 \\\\ \bze \end{Bmatrix}_O + \begin{Bmatrix} \Om\bz_0\\\\ \bze \end{Bmatrix}_O \end{equation*}
where we have used \(\bom_{2/0}= \Om \bz_0 - \dte \by_1\) and \(\vel_{O\in 2/0} = \bze\text{.}\) The kinetic energy of the system is found as follows
\begin{align*} \kin_{\Si/0} \amp = \kin_{\Si/0}^{(0)}+\kin_{\Si/0}^{(1)}+ \kin_{\Si/0}^{(2)} = \half I_1 \Om^2 + \half \bom_{2/0}\cdot \cI_{O,2} (\bom_{2/0})\\ \amp = \half I_1 \Om^2 + \half\begin{bmatrix}\Om \sin\te \\ -\dte \\ \Om \cos\te \end{bmatrix}\cdot \begin{bmatrix}A_2 \amp 0 \amp 0 \\0 \amp B_2 +mR^2 \amp 0\\0 \amp 0 \amp C_2+mR^2 \end{bmatrix}_{b_2} \begin{bmatrix} \Om \sin\te \\ -\dte \\ \Om \cos\te \end{bmatrix}\\ \amp = \half I_1 \Om^2 + \half A_2 \Om^2 \sin^2\te + \half (B_2 +mR^2) \dte^2 + \half (C_2+ mR^2) \Om^2 \cos^2 \te \end{align*}
where \([\cI_{O,2}]_{b_2}\) is obtained from \([\cI_{G, 2}]_{b_2}\) by using the Parallel Axis theorem. This leads to the expression of \(\kin_{\Si/0}^{(0)}\text{,}\) \(\kin_{\Si/0}^{(1)}\) and \(\kin_{\Si/0}^{(2)}\text{:}\)
\begin{equation*} \kin_{\Si/0}^{(0)} = \half I_1 \Om^2+ \half A_2 \Om^2 \sin^2\te +\half (C_2+ mR^2) \Om^2 \cos^2 \te, \end{equation*}
\begin{equation*} \kin_{\Si/0}^{(1)} =0 \end{equation*}
\begin{equation*} \kin_{\Si/0}^{(2)} = \half (B_2 +mR^2) \dte^2 \end{equation*}
Painlevé equation applied to system \(\Sigma\) can be written as
\begin{equation*} \frac{d}{dt}(\kin^{(2)}_{\Si/0} -\kin^{(0)}_{\Si/0} )+ \frac{\partial}{\partial t}\kin_{\Si/0} = \dte \qQ^{\te}_{\bSi\to \Si/0} + \dte \qQ^\te_{1 \leftrightarrow 2} \tag{1} \end{equation*}
with
\begin{equation*} \qQ^{\te}_{\bSi\to \Si/0} =\underbrace{\qQ^{\te}_{\bSi\to 1/0}}_{0} + \qQ^{\te}_{\bSi\to 2/0} = -\frac{\partial \pot}{\partial \te}= - mg R \cos\te \end{equation*}
using the gravitational potential \(\pot = mgR \sin\te\text{,}\) and
\begin{equation*} \qQ^\te_{1 \leftrightarrow 2} = \{ \cV^\te_{2/1} \} \cdot \{\cA^c_{1\to 2}\} = -\by_1 \cdot \bM^c_{O, 1\to 2} =0 \end{equation*}
The last result is a consequence of the fact that the joint between bodies 1 and 2 is ideal. Since the kinetic energy is not an explicit function of time, we find
\begin{equation*} \frac{\partial}{\partial t}\kin_{\Si/0} =0 \end{equation*}
Finally equation (1) becomes
\begin{equation*} \frac{d}{dt}(\kin^{(2)}_{\Si/0} -\kin^{(0)}_{\Si/0} ) = -\dte \frac{\partial\pot}{\partial \te} = -\frac{d\pot}{dt} \end{equation*}
This leads to Painlevé first integral
\begin{equation*} \kin^{(2)}_{\Si/0} -\kin^{(0)}_{\Si/0} + \pot = Cst \end{equation*}
or
\begin{equation*} (B_2 +mR^2) \dte^2 - \Big(I_1 + A_2 \sin^2\te + (C_2+ mR^2) \cos^2 \te \Big)\Om^2 + 2mgR \sin\te = Cst \tag{2} \end{equation*}
b. We can apply Lagrange equations to system \(\Si\) w.r.t. variables \((\psi, \te)\text{:}\) we then assume that the variables \((\psi,\te, \dpsi,\dte)\) are independent and must ignore the relationship \(\psi=\Om t\text{.}\) Now the kinetic energy of the system takes the expression
\begin{equation*} \kin_{\Si/0} = \half \Big(I_1 + A_2 \sin^2\te +(C_2+ mR^2) \cos^2 \te\Big) \dpsi^2 + \half (B_2 +mR^2) \dte^2 \end{equation*}
Lagrange equation \(\cL_{\Si/0}^\psi\) is given by
\begin{equation*} \frac{d}{dt} \Big( \big(I_1 + A_2 \sin^2\te +(C_2+ mR^2) \cos^2 \te \big) \dpsi \Big) = \qQ^\psi_{\bSi \to\Si /0} + \qQ^\psi_{1 \leftrightarrow 2} \end{equation*}
with
\begin{equation*} \qQ^\psi_{\bSi \to\Si /0} = \cC, \qquad \qQ^\psi_{1 \leftrightarrow 2} =0 \end{equation*}
This equation becomes:
\begin{equation*} \cL_{\Si/0}^\psi: \qquad \frac{d}{dt} \Big( \big(I_1 + A_2 \sin^2\te +(C_2+ mR^2) \cos^2 \te \big) \dpsi \Big) =\cC \tag{3} \end{equation*}
Similarly, Lagrange equation \(\cL_{\Si/0}^\te\) is given by
\begin{equation*} (B_2 +mR^2) \ddte - \Big(A_2 \sin\te\cos\te -(C_2+ mR^2) \cos\te\sin\te \Big) \dpsi^2 = \qQ^\te_{\bSi \to\Si /0} + \qQ^\te_{1 \leftrightarrow 2} \end{equation*}
with
\begin{equation*} \qQ^\te_{\bSi \to\Si /0} = - mg R \cos\te , \qquad \qQ^\te_{1 \leftrightarrow 2} =0 \end{equation*}
giving
\begin{equation*} \cL_{\Si/0}^\te: \;\; (B_2 +mR^2) \ddte - \Om^2 (A_2-C_2-mR^2)\sin\te\cos\te =- mg R \cos\te \tag{4} \end{equation*}
after substitution of \(\dpsi = \Om\text{.}\) It is easy to show that (4) can be obtained by taking the time-derivative of (2).
PrevTopNext