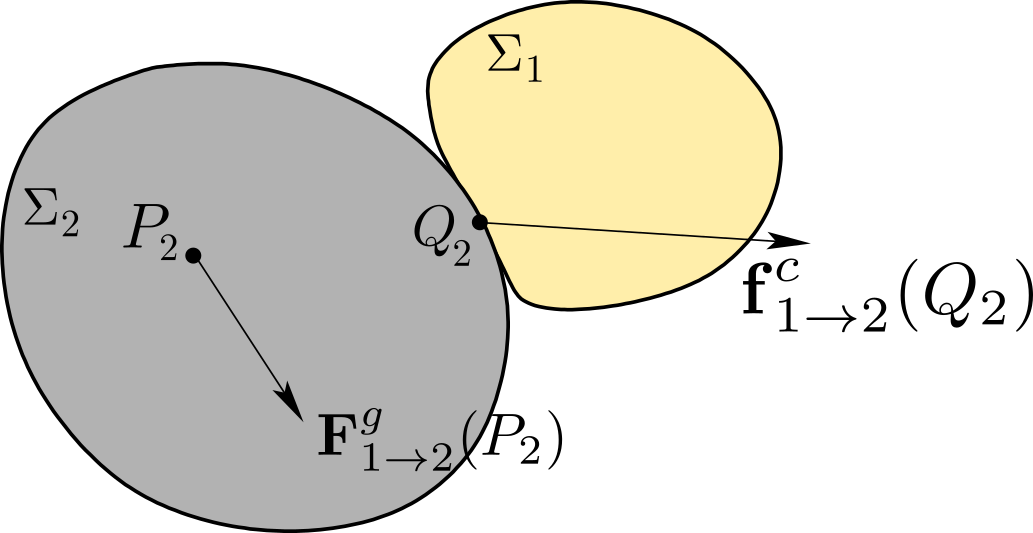
Section 12.2 Power of External Action
Recall that the power generated by a force
\(\bF\) acting on a particle
\(P\) moving at velocity
\(\vel_{P/\cE}\) relative to a referential
\(\cE\) is defined as the scalar
\(\bF \cdot \vel_{P/ \cE}\text{.}\) Let
\(\Sigma_1\) and
\(\Sigma_2\) be two material systems in mutual interaction under the effect of gravitational (or other action at-a-distance) forces
\(\bF ^g_{1 \rightarrow 2} (P_2)\) (
\(P_2 \in \Sigma_2\)) and contact forces
\(\bof^c_{1 \rightarrow 2} (Q_2)\) (
\(Q_2 \in \partial\Sigma_1 \cap \partial\Sigma _2\)) resulting in the action screws
\(\{ \cA^g _{\Sigma _1 \rightarrow \Sigma _2} \}\) and
\(\{ \cA^c_{\Sigma _1 \rightarrow \Sigma _2} \}\text{.}\) See
Figure 12.2.1.
Definition 12.2.2. Power of Mechanical Action.
The powers generated by the mechanical actions \(\{ \cA^g _{\Sigma _1 \rightarrow \Sigma _2}\}\) and \(\{ \cA^c_{\Sigma _1 \rightarrow \Sigma _2}\}\) during the motion of \(\Sigma _2\) relative to a referential \(\cE\text{,}\) are defined, at any given time, by
\begin{equation}
\Pow ^g _{ \Sigma _1 \rightarrow \Sigma _2 / \cE } =
\int_{\Sigma _2} \bF ^g_{1 \rightarrow 2} (P_2) \cdot \vel_{P_2/\cE} dV \tag{12.2.1}
\end{equation}
\begin{equation}
\Pow ^c _{ \Sigma _1 \rightarrow \Sigma _2 / \cE } =
\int_{\partial\Sigma_1 \cap \partial\Sigma _2}
\bof ^c_{1 \rightarrow 2} (Q_2) \cdot \vel_{Q_2/\cE} \, dA\tag{12.2.2}
\end{equation}
It is not possible in general to express these integrals in terms of the actions screws \(\{ \cA^g_{\Sigma _1 \rightarrow \Sigma _2} \}\) and \(\{ \cA^c_{\Sigma _1 \rightarrow \Sigma _2} \}\text{,}\) unless \(\Sigma_2\) is a rigid body. Assume that \(\Sigma_2\) is a rigid body denoted as \(\cB\text{.}\) Then the power generated by the forces exerted by \(\Sigma_1\) on rigid body \(\cB\) relative to a referential \(\cE\) can be expressed in terms of the corresponding action screw by taking advantage of the screw property of the velocity field \(P \in\cB \mapsto \vel_{\cB/\cE}\) as the product (comoment) between the action and kinematic screws:
Theorem 12.2.3. .
The power generated by the external actions exerted on rigid body \(\cB\) relative to referential \(\cE\) can be found as the scalar product between the action screw and the kinematic screw of \(\cB\text{:}\)
\begin{equation}
\Pow ^g _{ \Sigma _1 \rightarrow\cB / \cE }
=\{ \cA^g_{\Sigma _1 \rightarrow\cB} \}\cdot
\{ {\cal V}_{\cB/ \cE} \}
= \bR_{\Sigma _1 \rightarrow\cB}^g \cdot \vel_{A\in\cB /\cE} + \bM^g _{A,\Sigma _1 \rightarrow\cB}
\cdot \bom_{\cB /\cE}\tag{12.2.3}
\end{equation}
where \(\bR_{\Sigma _1 \rightarrow\cB}^{g}\) and \(\bM^{g} _{A,\Sigma _1 \rightarrow\cB}\) are the resultant and moment about arbitrary point \(A\) of action screw \(\{ \cA^{g}_{\Sigma _1 \rightarrow\cB} \}\text{.}\) Likewise, we have for the contact action
\begin{equation}
\Pow ^c _{ \Sigma _1 \rightarrow\cB / \cE } =
\{ \cA_{\Sigma _1 \rightarrow\cB}^c \}
\cdot
\{ {\cal V}_{\cB/ \cE} \} =
\bR_{\Sigma _1 \rightarrow\cB}^c \cdot \vel_{A\in\cB /\cE} + \bM^c _{A,\Sigma _1 \rightarrow\cB}
\cdot \bom_{\cB /\cE}\tag{12.2.4}
\end{equation}
Proof.
The expression of the virtual power defined as the integral
\(\int_{\cB} \vv_P \cdot \bF_{\Si_1 \to \cB}^g (P) dV\) in terms of the virtual velocity
\(P \mapsto \vv_P\) (which defines a virtual velocity screw
\(\{ \cV^* \}\)) was derived for the derivation of the FTD. See
Subsection 11.2.1. It was found to be given by
\(\{\cV^* \} \cdot \{ \cA^g_{\Sigma _1 \rightarrow\cB} \}\text{.}\) Here the virtual velocity
\(P \mapsto \vv_P\) is replaced by the velocity field
\(P\in\cB \mapsto \vel_P\) of rigid body
\(\cB\text{.}\) Hence, the volume integral of equation
(12.2.1) which defines the expression of power can be written in terms of the scalar product
\(\{ \cA^g_{\Sigma _1 \rightarrow\cB} \} \cdot\{ {\cal V}_{\cB/ \cE} \}\text{.}\)
The formalism of screws enables us to express the power
\(\Pow_{\Si_1 \to \cB /\cE}\) in a manner identical to the case of particles. More importantly, formulas
(12.2.3) and
(12.2.4) offer practical ways of determining expressions of powers generated by mechanical actions as demonstrated by the following examples.
Example 12.2.4.
Consider the rectangular plate
1 of
Example 11.2.17. It is constrained to rotate about a vertical fixed axis
\((O, \bz_0)\) of a referential
00. The pivot connecting
0 and
1 is assumed frictionless. A motor
\(\cM\) is mounted between
0 and
1 and its action on
1 is a constant couple
\(\cC \bz_0\text{.}\) In addition, the ambient fluid exerts a viscous force
\(d \bF (P) = - \mu \vel_{P/0} dA\) on an element of area
\(dA\) surrounding a point
\(P\) of the plate, where
\(\mu\) is a positive constant.
Determine the power generated by each contribution of the external action screw \(\{ \cA_{\bar{1}\to 1} \}\) exerted on body 1.
Solution.
The power generated by action screw
\(\{ \cA_{\bf \bar{1}\to 1} \}\) exerted on body
1 can be determined for each of the actions
\(\{\cA^g_{\text{Earth}\to 1}\}\text{,}\) \(\{\cA^c_{0 \to 1} \}\text{,}\) \(\{\cA_{\text{fluid}\to 1} \}\) and
\(\{\cA_{\cM\to 1}\}\) by applying formulas
(12.2.3) and
(12.2.4) using the expression
\begin{equation*}
\{ {\cal V} _{1/0} \} =
\begin{Bmatrix}
\dte \bz_0 \\\\
\bze
\end{Bmatrix}
_O
=
\begin{Bmatrix}
\dte \bz_0 \\\\
a\dte\by_1
\end{Bmatrix}
_G
\end{equation*}
of the kinematic screw of body 1. We obtain
\begin{align*}
\Pow_{\text{Earth}\to 1/0}^g
\amp =
\{\cA^g_{\text{Earth}\to 1}\} \cdot \{ {\cal V} _{1 / 0 } \} =
\begin{Bmatrix}
-m g \bz_0 \\
\\
\bze
\end{Bmatrix}
_G
\cdot
\begin{Bmatrix}
\dte \bz_0 \\
\\
a\dte\by_1
\end{Bmatrix}
_G \\
\amp =-m g \bz_0 \cdot a\dte\by_1 = 0
\end{align*}
\begin{equation*}
\Pow_{0\to 1/0}^c = \{\cA_{0 \to 1}^c \} \cdot \{ {\cal V} _{1/0} \} =
\underbrace{
\begin{Bmatrix}
\bR^c_{0\to 1} \\
\; \\
\bM^c_{O, 0\to 1}
\end{Bmatrix}
}_{\bM^c_{O, 0\to 1}\cdot \bz_0 = 0}
\cdot
\begin{Bmatrix}
\dte \bz_0 \\\\
\bze
\end{Bmatrix}_O
=
\bM^c_{O, 0\to 1}\cdot \dte \bz_0 =0
\end{equation*}
(taking into account that the pivot connection is frictionless)
\begin{align*}
\Pow_{\text{fluid}\to 1/0} \amp = \{\cA_{\text{fluid} \to 1} \}^c \cdot \{ {\cal V} _{1 / 0 } \}\\
\amp =- \mu ab
\begin{Bmatrix}
a \dte \by_1 \\
\; \\
a \dte ( -b \bx_1 + \tfrac{4}{3} a \bz_0)
\end{Bmatrix}_O
\cdot
\begin{Bmatrix}
\dte \bz_0 \\\\
\bze
\end{Bmatrix}_O \\
\amp =
- \tfrac{4}{3} \mu a^3 b \dte^2
\end{align*}
and finally
\begin{equation*}
\Pow_{\cM\to 1/0} = \{\cA_{\cM \to 1} \}^c \cdot \{ {\cal V} _{1 / 0 } \} =
\begin{Bmatrix}
\bze \\
\\
\cC \bz_0
\end{Bmatrix}
\cdot
\begin{Bmatrix}
\dte \bz_0 \\\\
\bze
\end{Bmatrix}_O
= \cC \dte
\end{equation*}
The total power is then found to be
\begin{equation*}
\Pow_{\bar{1}\to 1/0} = - \tfrac{4}{3} \mu a^3 b \dte^2+ \cC \dte
\end{equation*}
Example 12.2.6.
Consider the system of
Example 11.2.22. Disk
1 moves on a horizontal plane
\(\Pi\) of a referential
0 so that the extremity
\(O\) of its massless axle remains fixed in plane
\(\Pi\text{.}\) Furthermore friction between the disk and the plane
\(\Pi\) prevents slipping at both contact points
\(O\) and
\(I\text{.}\) See
Example 11.2.22 for notations.
Find the power \(\Pow_{\bar{1}\to 1/0}\) generated by all external actions on disk 1.
Solution.
Accounting for the contact forces at point \(O\) and \(I\text{,}\) and neglecting rolling and spinning friction, the external action screw exerted on body 1 takes the expression
\begin{equation*}
\{\cA_{\bar{1}\to 1} \}
=
\begin{Bmatrix}
\bR_O \\\\
\bze
\end{Bmatrix}
_{O}
+
\begin{Bmatrix}
\bR_I \\\\
\bze
\end{Bmatrix}
_{I}
+
\begin{Bmatrix}
-mg\be_3 \\\\
\bze
\end{Bmatrix}
_{C}
\end{equation*}
Furthermore, the kinematic screw of body 1 takes the expression, taking into account the no-slip conditions at \(O\) and \(I\text{:}\)
\begin{equation*}
\{ \cV _{1/0} \} =
\begin{Bmatrix}
- \dte \bu \\\\
\bze
\end{Bmatrix}
_{O}
=
\begin{Bmatrix}
- \dte \bu \\\\
\bze
\end{Bmatrix}
_{I}
=
\begin{Bmatrix}
- \dte \bu \\\\
{r\over\sqrt{2}} \dte \bv
\end{Bmatrix}
_{C}
\end{equation*}
\begin{align*}
\Pow_{\bar{1}\to 1/0} =
\begin{Bmatrix}
\bR_O \\\\
\bze
\end{Bmatrix}
_{O}
\cdot
\begin{Bmatrix}
- \dte \bu \\\\
\bze
\end{Bmatrix}
_{O}
\amp +
\begin{Bmatrix}
\bR_I \\\\
\bze
\end{Bmatrix}
_{I}
\cdot
\begin{Bmatrix}
- \dte \bu\\ \\
\bze
\end{Bmatrix}
_{I}\\
\amp + \begin{Bmatrix}
-mg\be_3 \\\\
\bze
\end{Bmatrix}
_{C}
\cdot
\begin{Bmatrix}
- \dte \bu \\\\
{r\over\sqrt{2}} \dte \bv
\end{Bmatrix}
_{C}
=0
\end{align*}
Denote by \(\Sigma = \{\cB_1 ,\cB_2, \ldots,\cB_N \}\) a system of \(N\) rigid bodies. Consider a material system \(\Sigma_1\) external to system \(\Sigma\) (\(\Sigma_1\subset\bSi\)) which acts upon each rigid body \(\cB_j\text{:}\) denote by \(\{\cA_{\Sigma _1 \rightarrow \cB _{j}} \}\) the corresponding action screw. We can then write:
\begin{equation*}
\Pow _{ \Sigma _1 \rightarrow \Sigma / \cE} =\sum _{j=1}^N
\Pow _{ \Sigma _1 \rightarrow\cB_j / \cE} =
\sum _{j=1}^N
\left\{ \cA_{\Sigma _1 \rightarrow\cB _{j}} \right\} \cdot
\left\{ {\cal V}_{\cB_{j} / \cE} \right\}
\end{equation*}
If the exterior \(\bSi\) is comprised of \(M\) material systems \(\Si_1\text{,}\) \(\Si_2\text{,}\) \(\ldots\text{,}\) \(\Si_M\text{,}\) then the total external power is found to be
\begin{equation*}
\Pow _{\bSi \rightarrow \Sigma / \cE} =
\sum _{j=1}^N
\Pow _{\bSi \rightarrow\cB_j / \cE} =\sum _{i=1}^M \sum _{j=1}^N
\Pow _{\Si_i \rightarrow\cB_j / \cE}
\end{equation*}