A pendulum is assembled by connecting a body
2 of mass center \(B\) and mass \(m\) to a slider 2 of mass center \(A\) and mass \(M\text{.}\) Slider 1 can translate without friction along the direction \(Ox\) of a referential 0 assumed Newtonian. Body 2 can rotate freely about a frictionless pivot at \(A\) relative to the slider. The motion of the system occurs in a vertical plane. The slider can be set in a initial position either sufficiently far from a vertical backstop or in contact with it. The pendulum is initially displaced at some angle \(-\pi / 2 \leq \te_0 \lt 0\text{,}\) defining positive angle \(\theta\) in the anticlockwise direction. The system slider/pendulum is then released without initial speed.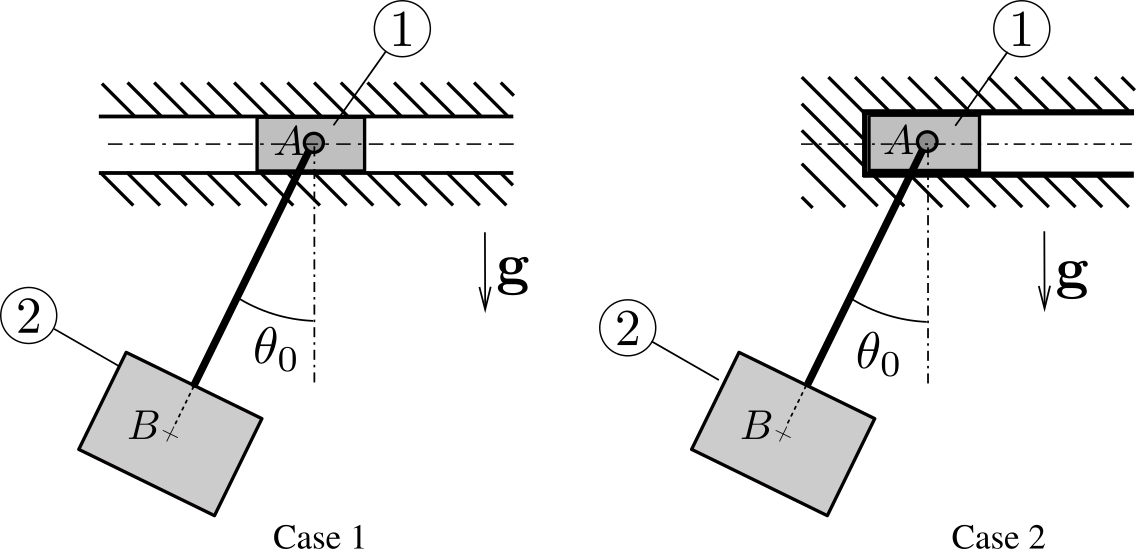
Its position at any time \(t\) is defined by the coordinate \(x(t)\) of \(A\) measured along axis \(Ox\) and by the angle \(\te(t)\text{.}\) Denote by \(l\) the distance \(AB\) and by \(J =mk^2\) the moment of inertia of pendulum
2 about its axis of rotation.- Case 1. The slider is set in a initial position sufficiently far from the backstop. Find the relationship between \(\dx\) and \(\dte\text{.}\) Describe the motion of the system. Describe the motion of the mass center \(G\) of the system. Along which curve does point \(B\) evolve? Find the period of the small amplitude oscillations of the system.
- Case 2. The slider is now set initially in contact with the backstop. Find the relationship between \(\dx\) and \(\dte\text{.}\) Show that initially the slider remains in contact with the backstop. When does this contact cease? Show that after contact ceases, the slider never comes back to the backstop. Carefully describe the motion of the system.
Solution.
-
Case 1. Define the fixed unit vectors \((\be_x , \be_y , \be_z )\) with \(\be_x\) along horizontal axis \(Ox\text{,}\) \(\be_z\) vertical downward, and \(\be_y = \be_z \times \be_x\) perpendicular to the plane of motion. See Figure 11.3.3. The position of the system is defined by coordinate \(x(t)\) of \(A\) along axis \(Ox\) and by the oriented angle \(\te (t)\) which line \(AB\) makes with the vertical. Introduce unit vector \(\bu\) along line \(AB\) directed from \(A\) to \(B\text{,}\) and \(\bv = \be_y \times \bu\text{.}\) The position vectors of \(A\) and \(B\) are then given by\begin{equation*} \br_{OA} = x \be_x , \qquad \br_{OB} = x \be_x + l \bu. \end{equation*}Then the velocities of \(A\) and \(B\) are given by\begin{equation*} \vel_A = \dx \; \be_x , \qquad \vel_B = \dx \; \be_x + l \dte \bv . \end{equation*}At time \(t=0\text{,}\) we have \(\te = \te_0\text{,}\) and \(\dx = 0\) and \(\dte =0\) since the system is released without initial velocity.
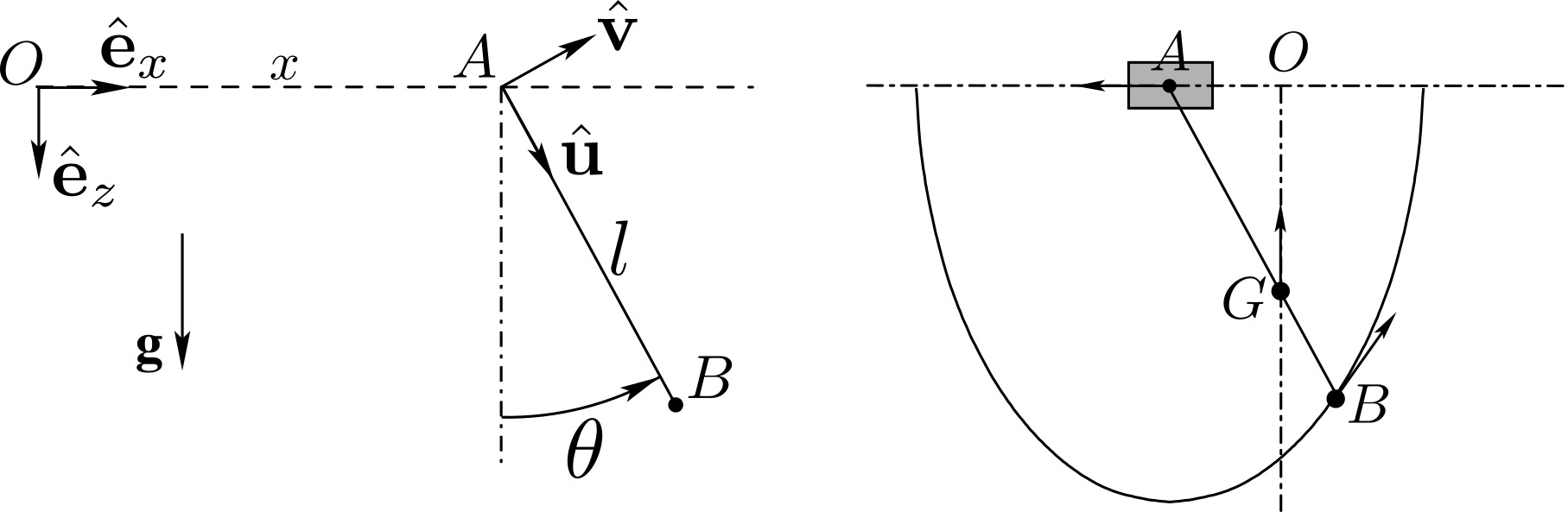
Figure 11.3.3. Denote by \(\Sigma\) the system slider/pendulum and by \(G\) its mass center. The external forces acting on \(\Sigma\) are the gravitational forces \(M \bg\) and \(m \bg\text{,}\) and the reaction force \(N \be_z \) directed along \(\be_z \) in the absence of friction. Hence, the resultant force \(\bF_{\bSi\to\Si}\) on \(\Sigma\) satisfies \(\bF_{\bSi\to\Si} \cdot \be_x =0\text{.}\) This implies that \((m+M) \ba_G \cdot \be_x =0\) and by integration that (\(\be_x\) is a constant unit vector)\begin{equation*} (m+M) \vel_G \cdot \be_x = \text{constant} = 0 \end{equation*}The constant of integration vanishes since the initial velocity of the system is zero. Hence, there is conservation of the linear momentum of \(\Sigma\) on axis \(Ox\). With \((M+m) \vel_G = M \vel_A + m \vel_B\text{,}\) we obtain\begin{equation*} ( M \vel_A + m \vel_B) \cdot \be_x = (M+m ) \dx + m l \dte \cos\te = 0 \qquad{(1)} \end{equation*}This equation shows that the sign of \(\dx\) (which gives the direction taken by the slider) is the sign of \((- \dte \cos\te)\text{.}\) Since we expect the angle \(\te\) to remain in the interval \(- \pi /2 \lt \te \lt \pi /2\text{,}\) we have \(\text{sign} (\dx) = - \text{sign}(\dte)\text{:}\) if the pendulum rotates in the clockwise direction \((\dte \lt 0)\text{,}\) then the slider moves forward \((\dx > 0)\text{.}\) Conversely, if it rotates in the counterclockwise direction \((\dte \gt 0)\text{,}\) then the slider moves backward \((\dx \lt 0)\text{.}\)The mass center \(G\) of the system moves along a vertical line since from equation (1) \(\vel_G \cdot \be_x =0\text{:}\) we get by integration \(\br_{OG} \cdot \be_x = \text{constant}\text{.}\) The position of \(B\) is given by \(\br_{OB}= (x + l \sin \te) \be_x + l \cos\te \be_z\text{,}\) where \(x = - { m \over m+M} l \sin\te\) by integration of (1) assuming \(x= 0\) when \(\te =0\text{.}\) The coordinates of \(B\) are then given by\begin{equation*} x_B = {M \over M+m} l \sin\te, \qquad z_B = l \cos\te \end{equation*}Eliminating \(\te\) gives the Cartesian equation of the trajectory of \(B\text{:}\)\begin{equation*} \left( {x_B \over l( 1 + {m\over M}) } \right)^2 + \left( {z_B \over l} \right)^2 = 1 \end{equation*}This equation is that of an ellipse.To find the period of small oscillations, we need a second equation: we apply the moment equation for pendulum2about point \(A\text{:}\)\begin{equation*} \be_y \cdot \bD_{A, 2/0} = \be_y \cdot \bM_{A, \bar{2}\to 2} = \be_y \cdot (\br_{AB} \times mg\be_z )= -mgl \sin\te \end{equation*}with \(\bD_{A, 2/0} = d\bH_{A, 2/0} /dt + \vel_A \times m\vel_G\) and \(\bH_{A , 2/0} \cdot\be_y = J \dte + \be_y \cdot (m \br_{AB}\times \vel_A) = J\dte + m l\dx\cos\te\text{.}\) This gives our second equation of motion\begin{equation*} J\ddte + ml \ddx \cos\te = -mgl \sin\te \qquad{(2)} \end{equation*}Assuming that the initial angle \(\te_0\) is small, the angle \(\te\) and its derivative \(\dte\) remain small at all time. Using the approximations \(\sin\te \approx \te\) and \(\cos\te\approx 1\text{,}\) we obtain a linear approximation of this equation\begin{equation*} \Big( k^2 - \frac{m}{m+M} l^2 \Big) \ddte + {gl} \te =0 \end{equation*}The period of the oscillations of the system is then\begin{equation*} T = 2\pi \sqrt{ \frac{gl}{k^2- \frac{m}{m+M} l^2 } } \end{equation*}Note that \(k\) is necessarily larger than \(l \sqrt{\frac{m}{m+M}}\text{.}\) -
Case 2.If the slider is initially in contact with the backstop, we can expect an initial phase during which it remains in contact with the backstop: indeed as the angle increases from the initial value \(\te_0 \lt 0\text{,}\) the slider has a tendency to move backward. Hence, we can assume that there exists an initial phase during which \(\dx = 0\) and the external force exerted to system \(\Sigma\) is augmented by a horizontal reaction \(R \bx\) due to the backstop. As long as \(R > 0\text{,}\) contact is maintained. If \(R (t) = 0\) at some time \(t_1\text{,}\) then the slider ceases to be in contact with the backstop. During the first phase, the motion of \(\Sigma\) along the \(x\)-axis is governed by the equation\begin{align*} R \amp = (m+M) \ba_G \cdot \be_x = {d\over dt} [ (m+M) \dx + ml \dte \cos\te ]\\ \amp = ml (\ddte \cos\te - \dte^2 \sin\te ) \end{align*}We can predict the sign of \(R\) without having to find the angular acceleration \(\ddte\) and the angular velocity \(\dte\) as a function of \(\te\text{.}\) Indeed the angular acceleration \(\ddte\) is positive (\(\dte\) increases) in the range \(\te_0 \leq \te \lt 0\text{,}\) becomes zero for \(\te = 0\text{,}\) and is negative for \(\te > 0\text{.}\) Hence \({\rm sign}(\ddte ) = - {\rm sign} (\sin\te)\text{.}\) This shows that\begin{equation*} \left\{ \begin{array}{lr} R \gt 0 , \amp \qquad \te_0 \leq \te \lt 0 \\ R = 0 , \amp \qquad \te = 0 \\ R \lt 0 , \amp \qquad \te \gt 0 \end{array} \right. \end{equation*}Hence the slider ceases to be in contact with the backstop the moment the pendulum crosses the vertical. The instant \(t_1\) at which this occurs is of course a function of the initial angle \(\te_0\text{.}\) In the second phase (\(t \geq t_1\)), once contact with the backstop ceases, we are in a similar situation as in case 1: there is conservation of linear momentum of \(\Sigma\) along axis \(Ox\text{.}\) In this case, however, the linear momentum of \(\Sigma\) along axis \(Ox\) is not zero since\begin{equation*} (m+M) \vel_{G} \cdot \be_x = {\rm constant} = m \vel_B (t_1) \cdot\be_x = m l \dte_1 \end{equation*}where the constant of the motion is obtained at time \(t=t_1\text{:}\) \(\dte = \dte_1\) and \(\dx =0\text{.}\) Hence in the second phase, the mass center of \(\Sigma\) moves uniformly in the direction of axis \(Ox\). Furthermore, the slider’s velocity \(\dx\) is given by\begin{equation*} \dx = {m \over M+m} l ( \dte_1 - \dte \cos\te ) \end{equation*}We expect in phase 2 that \(\dte \leq \dte_1\) and that \(\dte = \dte_1 > 0\) at \(\te =0\text{.}\) This shows that the slider velocity remains positive and becomes zero whenever the pendulum crosses the vertical with a positive velocity. Hence the slider always moves forward in a non-uniform way in the \(x\text{.}\)direction, coming to a stop whenever the pendulum crosses the vertical in the forward direction. It never comes back toward the backstop. The situation is thus quite different from that of case 1.