Skip to main content

Advanced Engineering Dynamics

R. Valéry Roy

Section 13.5 Lagrange Equations: System of Rigid Bodies

Consider a system \(\Si\) of \(p\) rigid bodies \((\cB_1 , \ldots, \cB_p)\) in motion in a Newtonian referential \(\cE\text{.}\) The configuration of the system is defined by \(n\) coordinates \((q_1, \ldots, q_n)\) and by time \(t\) satisfying assumption (13.1.2). All holonomic and non-holonomic equations which may govern these coordinates are therefore ignored. The simplest way to derive the \(n\) Lagrange equations governing \(\Sigma\) is to add the \(p\) equations written for each rigid body \(\cB_\jmath\text{:}\) we obtain for a given coordinate \(q_i\)  1 
\begin{equation} \left[\frac{d}{dt}\left(\frac{\partial}{\partial \dq_i}\right) - \frac{\partial}{\partial q_i} \right] (\kin_{1/0} + \kin_{2/0} + \cdots + \kin_{p/0}) = \sum_{\jmath=1}^p \qQ_{\bar{\jmath}\to \jmath /0} ^{q_i}\tag{13.5.1} \end{equation}
We then write the actions on body \(\cB_\jmath\) as a sum of contributions internal and external to the system
\begin{equation*} \{\cA_{\bar{\jmath}\to \jmath}\} =\{\cA_{\bSi\to \jmath}\} + \sum_{k=1}^p \{\cA_{k \to \jmath}\} \end{equation*}
Then equation (13.5.1) becomes
\begin{equation*} \left[\frac{d}{dt}\left(\frac{\partial}{\partial \dq_i}\right) - \frac{\partial}{\partial q_i} \right] \kin_{\Si/0} = \qQ_{\bSi\to \Si /0} ^{q_i} + \sum_{\jmath,k=1}^p \qQ_{k \to \jmath /0} ^{q_i} \end{equation*}
where we have written the system’s kinetic energy as \(\kin_{\Si/0} =\kin_{1/0} + \cdots + \kin_{p/0}\text{.}\) Consider a pair of interacting bodies \(\cB_\jmath\) and \(\cB_k\) (fixing \(q_i\text{.:}\) we recognize the sum \(\qQ_{k \to \jmath /0} ^{q_i} + \qQ_{\jmath \to k/0} ^{q_i}\) as the \(q_i\)-power coefficient of interaction between \(\cB_\jmath\) and \(\cB_k\text{:}\)
\begin{align*} \qQ_{k \to \jmath /0} ^{q_i} + \qQ_{\jmath \to k/0} ^{q_i}\amp =\{\cA_{k \to \jmath}\}\cdot\{\cV^{q_i}_{\jmath/0}\}+ \{\cA_{\jmath \to k}\}\cdot\{\cV^{q_i}_{k/0}\}\\ \amp =\{\cA_{k \to \jmath}\}\cdot \left( \{\cV^{q_i}_{\jmath/0}\}- \{\cV^{q_i}_{k/0}\}\right)= \{\cA_{k \to \jmath}\}\cdot \{\cV^{q_i}_{\jmath/k}\}\\ \amp =\qQ_{k \leftrightarrow \jmath} ^{q_i} \end{align*}
Then we write the sum of internal terms as a pairwise sum
\begin{equation*} \sum_{\jmath,k=1}^p \qQ_{k \to \jmath /0} ^{q_i} = \sum_{1\leq \jmath \lt k \leq p}\qQ_{k \leftrightarrow \jmath} ^{q_i} \end{equation*}
In conclusion, the Lagrange equations for system \(\Si\) can be stated as follows:

Remark 13.5.2.

A special case of Theorem 13.5.1 can be formulated as follows:
  1. if all joints between the bodies of system \(\Si\) are ideal,
  2. if all joints between \(\Si\) and external bodies which are either fixed or whose motions are prescribed, are ideal,
  3. if all other actions, whether external or internal, derive from potential energies \(\pot =\pot_{\bSi\to \Si/0}+ \sum_{\jmath \lt k} \pot_{k \leftrightarrow \jmath}\text{,}\)
then Lagrange equations can be stated as follows:
\begin{equation} \left[\frac{d}{dt}\left(\frac{\partial}{\partial \dq_i}\right) - \frac{\partial}{\partial q_i} \right] \lag_{\Si/0} = 0\tag{13.5.3} \end{equation}
where \(\lag_{\Si/0} = \kin_{\Si/0} - \pot\) is known as the Lagrangian of the system.

Remark 13.5.3.

It is possible that one (or more) Lagrange equation leads to a first integral of motion if the following conditions are met:
  1. all external actions satisfy \(\qQ_{\bSi\to \Si /0} ^{q_1} =0\text{,}\)
  2. all internal interactions satisfy \(\qQ_{k \leftrightarrow \jmath} ^{q_1} =0\text{,}\)
  3. the kinetic energy \(\kin_{\Si/0}\) is not explicitly a function of \(q_1\text{,}\)
then Lagrange equation \(\cL^{q_1}_{\Si/0}\) leads to
\begin{equation*} \frac{\partial}{\partial \dq_1} \kin_{\Si/0} = \text{Cst} \end{equation*}
Here is an illustration of Lagrange equations (13.5.2).

Example 13.5.4.

We consider the motion of a system \(\Sigma\) comprised of an axisymmetric body 2 connected to a ring-like rigid body 1 in motion on a fixed horizontal plane \(\Pi (O, \bx_0, \by_0)\text{.}\) More specifically, body 1 (of mass center \(G\text{,}\) of mass \(m_1\text{.}\) rolls without slipping on plane \(\Pi\) in such a way as to remain vertical. We denote by \((G, \by_1)\) the axis of 1. Unit vector \(\bz_1\) shown in Figure 13.5.5 is directed along a particular diameter of 1 which coincides with the axis of body 2. Let \(I\) be the contact point of body 1 with \(\Pi\text{,}\) and let \((x,y, R)\) be the Cartesian coordinates of \(G\) relative to referential 0\((O, \bx_0 , \by_0, \bz_0)\text{.}\) The orientation of 1 relative to 0 is defined by
  1. angle \(\psi\) which defines the orientation of the vertical plane containing 1 relative to 0,
  2. angle \(\theta\) which defines the orientation of axis \((G,\bz_1)\) relative to the vertical plane containing 1.
The inertia matrix of body 1 about \(G\) takes the form
\begin{equation*} [\cI_{G,1}]_{b_1} = \begin{bmatrix} I_1 \amp 0 \amp 0 \\ 0 \amp J_1 \amp 0 \\ 0 \amp 0 \amp I_1 \end{bmatrix}_{b_1} \end{equation*}
on basis \(b_1 (\bx_1,\by_1,\bz_1)\text{.}\)
Body 2 (of mass center \(G\text{,}\) mass \(m_2\text{.}\) is mounted on the diameter \((G,\bz_1)\) through a frictionless pivot about which it is free to rotate. Denote by \(\phi\) the angle of rotation of 2 relative to 1 measured about axis \((G, \bz_1)\text{.}\) Its inertia matrix about \(G\) takes the form
\begin{equation*} [\cI_{G,2}]_{b_2} = \begin{bmatrix} I_2 \amp 0 \amp 0 \\ 0 \amp I_2 \amp 0 \\ 0 \amp 0 \amp J_2 \end{bmatrix}_{b_2} \end{equation*}
on basis \(b_2 (\bx_2,\by_2, \bz_1)\) attached body 2.
Figure 13.5.5.
  1. Find the equations which express the no-slip condition of body 1 at point \(I\text{.}\)
  2. Assume that the contact at \(I\) is realized with (sliding) friction (neglecting spinning and rolling friction), and that the corresponding action screw takes the form
    \begin{equation*} \{ \cA_{\Pi \to 1} \}^c = \begin{Bmatrix} X \bx_0 + Y \by_0 + Z\bz_0 \\\\ M \bu \end{Bmatrix} _I \end{equation*}
    where the (unknown) couple \(M \bu\) accounts for the fact that body 1 is maintained vertical. Find the five Lagrange equations \(\cL^q_{\Si/0}\) with respect to coordinates \(q= x,y,\psi, \theta, \phi\text{.}\) Can unknown couple \(M\) be found?
  3. A massless motor is mounted between bodies 1 and 2 to exert a couple \(\cC \bz_1\text{:}\) find the corresponding change in the Lagrange equations found in question b).
Solution.
a. We find the slip velocity at \(I\) according to \(\vel_{I\in 1/0}= \vel_{G/0}+ \bom_{1/0} \times \br_{GI}\text{:}\)
\begin{equation*} \vel_{I\in 1/0} = \dx \bx_0 + \dy \by_0 + (\dpsi \bz_0 + \dte \by_1)\times (-R\bz_0)= \dx \bx_0 + \dy \by_0 - R\dte \bu \end{equation*}
The no-slip condition then gives two equations
\begin{align*} \dx \amp = R \dte\cos\psi \amp \qquad\qquad (1) \\\\ \dy \amp = R \dte\sin\psi \amp \qquad\qquad (2) \end{align*}
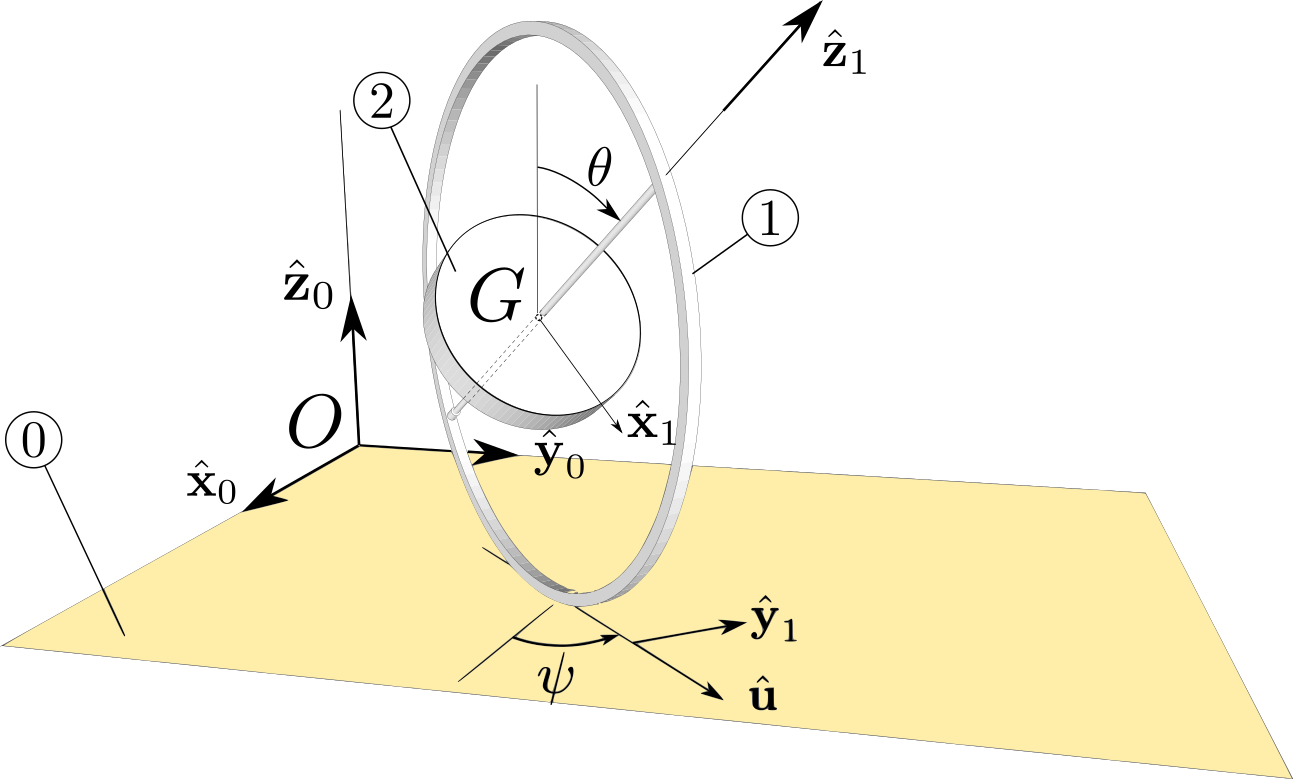
b. We assume that the coordinates \((x,y,\psi,\theta, \phi)\) satisfy the assumption (13.1.2). We then find the kinematic screws \(\{\cV_{1/0} \}\text{,}\) \(\{\cV_{2/1}\}\) and \(\{ \cV_{2/0} \}\)
\begin{equation*} \{\cV_{1/0} \} = \begin{Bmatrix} \dpsi \bz_0 + \dte \by_1 \\\\ \dx \bx_0 +\dy \by_0 \end{Bmatrix}_G =\begin{Bmatrix} \dpsi \bz_0 + \dte \by_1 \\\\ \dx \bx_0 +\dy \by_0 -R \dte \bu \end{Bmatrix}_I \end{equation*}
\begin{equation*} \{\cV_{2/1} \} = \begin{Bmatrix} \dphi \bz_1 \\\\ \bze \end{Bmatrix}_G \qquad \{\cV_{2/0} \} = \{\cV_{2/1} \}+\{\cV_{1/0} \} = \begin{Bmatrix} \dpsi \bz_0 + \dte \by_1+\dphi \bz_1 \\\\ \dx \bx_0 +\dy \by_0 \end{Bmatrix}_G \end{equation*}
We can then determine the expression of the partial kinematic screws \(\{\cV_{1/0}^q \}\text{,}\) \(\{\cV_{2/1}^q \}\) and \(\{\cV_{2/0}^q \}\) for \(q= x,y, \psi,\theta, \phi\text{.}\) The power coefficients \(\qQ^q_{\bar{1}\to 1/0}\text{,}\) \(\qQ^q_{\bar{2}\to 2/0}\text{,}\) and \(\qQ^q_{1\leftrightarrow 2}\) are then found to be
\begin{equation*} \qQ^q_{\bar{1}\to 1/0} = \begin{Bmatrix} X \bx_0 + Y \by_0 + (Z-mg)\bz_0 \\\\ M \bu \end{Bmatrix}_I \cdot \frac{\partial}{\partial \dq} \begin{Bmatrix} \dpsi \bz_0 + \dte \by_1 \\\\ \dx \bx_0 +\dy \by_0 -R \dte \bu \end{Bmatrix}_I \end{equation*}
leading to
\begin{equation*} \qQ^q_{\bar{1}\to 1/0} = \left\{ \begin{array}{ll} X \amp , \quad q=x\\ Y \amp , \quad q=y\\ 0 \amp , \quad q=\psi,\phi\\ -R(X\cos\psi+ Y\sin\psi) \amp ,\quad q=\theta \end{array} \right. \end{equation*}
\begin{equation*} \qQ^q_{\bar{2}\to 2/0} = \begin{Bmatrix} -mg\bz_0 \\ \bze \end{Bmatrix}_G \cdot \frac{\partial}{\partial \dq} \begin{Bmatrix} \dpsi \bz_0 + \dte \by_1+\dphi \bz_1 \\\\ \dx \bx_0 +\dy \by_0 \end{Bmatrix}_G = 0, \quad q= x,y, \psi,\theta, \phi \end{equation*}
\begin{equation*} \qQ^q_{1\leftrightarrow 2} =\{ \cA_{1 \to 2} \}^c \cdot \frac{\partial}{\partial \dq} \begin{Bmatrix} \dphi \bz_1 \\\\ \bze \end{Bmatrix}_G = \left\{ \begin{array}{l l} 0 \amp , \quad q=x,y,\psi,\theta \\ \bM_{G, 1\to 2}^c \cdot \bz_1 =0 \amp ,\quad q=\phi\\ \end{array} \right. \end{equation*}
The next step is to find the kinetic energy of the system:
\begin{align*} 2\kin_{\Si/0} \amp = (m_1+m_2)\vel_{G/0}^2 + \bom_{1/0} \cdot \cI_{G,1}(\bom_{1/0}) + \bom_{2/0} \cdot \cI_{G,2}(\bom_{2/0})\\ \amp = (m_1+m_2)(\dx^2 + \dy^2) + (I_1+I_2 \sin^2\te+ J_2 \cos^2\te)\dpsi^2 + (J_1+I_2) \dte^2 + J_2 \dphi^2 + 2J_2 \dphi\dpsi \cos\te \end{align*}
We can now apply (13.5.2) for system \(\Sigma\) to find seven Lagrange equations:
\begin{align*} \cL^{x}_{\Si/0}:\amp \quad m \ddx = X \amp {(3)}\\\\ \cL^{y}_{\Si/0}:\amp \quad m \ddy = Y \amp {(4)}\\\\ \cL^{\psi}_{\Si/0}:\amp \quad (I_1+I_2 \sin^2\te+ J_2 \cos^2\te)\dpsi +J_2 \dphi \cos\te = const. \amp {(5)}\\\\ \cL^{\te}_{\Si/0}:\amp \quad (J_1+I_2) \ddte - (I_2-J_2) \dpsi^2 \cos\te\sin\te +J_2 \dphi\dpsi \sin\te = -R(X\cos\psi+ Y\sin\psi) \amp {(6)}\\ \cL^{\phi}_{\Si/0}:\amp \quad \dphi + \dpsi \cos\te = const. \amp {(7)} \end{align*}
Equations (1-7) solve for seven unknowns \((x,y, \psi,\theta, \phi, X, Y)\text{.}\) However moment \(M\) remains unknown. To find it, it is best to use the Newton-Euler approach: it is immediately seen that the following dynamic moment equation solves for \(M\)
\begin{equation*} \bD_{I, \Si/0} \cdot \bu = M = \bD_{I, 1/0} \cdot \bu+\bD_{I, 2/0} \cdot \bu \end{equation*}
with
\begin{align*} \bD_{I, 1/0} \cdot \bu \amp = \bu\cdot \left( \frac{d}{dt}\bH_{G,1/0} +\br_{IG}\times m_1 \ba_{G/0} \right)\\ \amp = \bu \cdot \frac{d}{dt}(I_1 \dpsi \bz_0 + J_1 \dte \by_1) + \bu \cdot R\bz_0 \times m_1 R(\ddte \bu+ R\dte^2 \by_1)\\ \amp = -(J_1 + m_1 R^2 ) \dte^2 \end{align*}
and
\begin{align*} \bD_{I, 2/0} \cdot \bu \amp = \bu\cdot\left( \frac{d}{dt}\bH_{G,2/0} + \br_{IG}\times m_2 \ba_{G/0}\right) \\ \amp = \bu \cdot \frac{d}{dt}[-I_2 \dpsi \sin\te\bx_1 + I_2 \dte \by_1 +J_2 (\dphi+ \dpsi\cos\te)\bz_1] - m_2 R^2 \dte^2 \\ \amp = -(I_2 + m_2 R^2 ) \dte^2 +\frac{d}{dt}[J_2\dphi + (J_2 -I_2) \cos\te\sin\te] \end{align*}
This gives the expression of \(M\text{:}\)
\begin{equation*} M= -(J_1 +I_2+ (m_1+m_2) R^2 ) \dte^2 + \frac{d}{dt}[J_2\dphi + (J_2 -I_2) \cos\te\sin\te] \end{equation*}
c. The addition of the motor between bodies 1 and 2 contributes to an additional term for the power coefficient of interaction \(\qQ^\phi_{1\leftrightarrow 2}\)
\begin{equation*} \qQ^\phi_{1\leftrightarrow 2} =\{ \cA_{1 \to 2} \}^c \cdot \frac{\partial}{\partial \dphi} \begin{Bmatrix} \dphi \bz_1 \\\\ \bze \end{Bmatrix}_G = (\cC \bz_1 +\bM_{G, 1\to 2}^c) \cdot \bz_1 =\cC \end{equation*}
The only modified Lagrange equation is \(\cL^{\phi}_{\Si/0}\text{:}\)
\begin{equation*} \cL^{\phi}_{\Si/0}: \qquad \cC = J_2 \frac{d}{dt}(\dphi + \dpsi \cos\te ) \quad {(7')} \end{equation*}
PrevTopNext