1.
A spherical body
1 of mass \(m\) moves along a horizontal support \(Ox\) of a referential 0 assumed Newtonian. The contact is characterized by coefficient of kinetic friction \(\mu\) and coefficient of rolling friction \(k\text{.}\) The initial condition corresponds to a forward motion of its mass center \(G\) at speed \(v_0\) and backspin at angular speed \(\om_0\text{.}\)
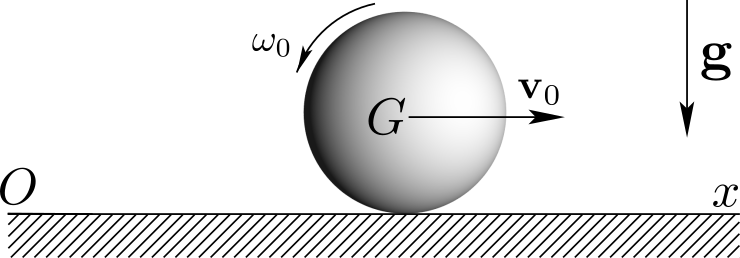
Analyze the motion of body
1.Solution.
The kinematics of body
1 relative to referential 0 \((O,\be_x , \be_y , \be_z)\) is entirely specified by the velocity \(\vel_G = v_G (t) \be_x\) of its mass center, and by its angular velocity \(\bom = \om (t) \be_z\text{.}\) Then the slip velocity of the body is given by
\begin{equation*}
\vel_{I \in 1/0} = \vel_G + \bom \times \br_{GI} = (v_G + r \om ) \be_x
\qquad{(1)}
\end{equation*}
At time \(t=0\text{,}\) the slip velocity takes the expression \(\vel_{I\in 1/0} = (v_0 + r\om_0) \be_x\text{.}\) Since \((v_0+ r\om_0 ) \gt 0\text{,}\) the sphere initially slips, and we can assume that the initial phase of motion is also characterized by slipping.

The external forces acting on body
1 are (i) the gravitational force \(m \bg\) applied at mass center \(G\text{,}\) and (ii) the contact actions assuming sliding and rolling friction. This gives the total action screw
\begin{equation*}
\{\cA_{ \bar{1}\to 1} \} =
\left\{
\begin{array}{c}
- m g \be_y \\
\bze
\end{array}
\right\}_G
+
\left\{
\begin{array}{c}
F\be_x + N\be_y \\
M_I \be_z
\end{array}
\right\}_I
\end{equation*}
Application of the FTD \(\{\cA_{ \bar{1}\to 1}\} = \{ \cD_{1 /0} \}\) gives:
- the resultant equation \(m \ba_G = m \bg + F\be_x +N\be_y\text{,}\) or by projection on \((\be_x , \be_y )\text{,}\)\begin{equation*} m \dot{v}_G = F , \qquad N = mg \qquad (2-3) \end{equation*}
- the moment equation about point \(G\) (mass center of
1) \(\bD_G = \bM_G\text{,}\) or, with \(\bD_G = (d\bH_G /dt) = {2\over 5} mr^2 \dom \be_z\) and \(\bM_G = (rF +M_I)\be_z\text{,}\)\begin{equation*} {2\over 5} mr^2 \dom = r F+M_I \qquad (4) \end{equation*}
We have obtained 3 equations solving for 5 unknowns \(v_G\text{,}\) \(\om\text{,}\) \(F\text{,}\) \(N\) and \(M_I\text{.}\) We need two additional equations. They are provided by Coulomb laws:
- We have \(F = - \mu N = -\mu mg\text{,}\) since the friction force \(F \be_x\) must oppose the slip velocity \(\vel_{I\in 1/0}\) (initially \(v_0 + r \om_0 \gt 0\)).
- We also state that \(M_I = -k N = -k mg\) since moment \(M_I\) must oppose the rolling motion (initially \(\om_0 \gt 0\)).
Now we solve equations (2-4):
\begin{equation*}
\dom = - {5g \over 2r} (\mu + {k \over r}), \qquad \dv_G = - \mu g
\end{equation*}
showing that both \(v_G\) and \(\om\) are (linearly) decreasing functions of time. Eventually the slip velocity will reach the zero value. We obtain by integration
\begin{equation*}
\boxed{
\om (t)= \om_0 - {5g \over 2r} (\mu + {k \over r}) t , \quad
v_G (t) = v_0 - \mu g t
}
\end{equation*}
leading to the slip velocity
\begin{equation*}
\vel_{I \in 1/0} (t) = ( v_0 + r\om_0 - {7\mu r+5k \over 2r} g t)\be_x .
\end{equation*}
The slip of body
1 ceases at time
\begin{equation*}
\boxed{
t_1 = {2 \over g} {v_0 + r \om_0 \over 7\mu +5k/r}
}
\end{equation*}
Time \(t_1\) corresponds to the start of the no-slip phase of motion of the spherical body: once it stops slipping, it continues to roll without slipping. At time \(t=t_1\text{,}\) mass center \(G\) takes the velocity
\begin{equation*}
v_1 = v_0 - \mu g t_1
\end{equation*}
and body
1 has the angular velocity
\begin{equation*}
\om_1 = \om_0 - {5g \over 2r} (\mu+ {k \over r}) t_1
\end{equation*}
At this point, the sphere may roll forward, stop or roll backward.
For \(t \geq t_1\text{,}\) the sphere rolls without slipping: \(\vel_{I\in 1/0} = \bze\text{.}\) The translational and rotational motion of \(\cB\) are now coupled:
\begin{equation*}
v_G = - r\om , \qquad t \geq t_1 \qquad (5)
\end{equation*}
Assume that the sphere rolls forward: \(v_G \gt 0\) and \(\om \lt 0\text{.}\) The motion is still governed by the equations (2-4). Now with equation (5), we find
\begin{equation*}
F = m \dv_G = - mr \dom = {2\over 5}mr \dom - {M_I \over r}
\end{equation*}
Since \(\om \lt 0\text{,}\) we must have \(M_I = kmg \gt 0\text{.}\) We can integrate to obtain \(\om (t)\) for \(t \geq t_1\text{:}\)
\begin{equation*}
r\om = r\om_1 + {5k \over 7r} gt = -v_G , \qquad t \geq t_1 .
\end{equation*}
Then we find that the motion ends at time \(t=t_2\) given by
\begin{equation*}
\boxed{
t_2 = - {7 r\om_1 \over g} {r\over k}
}
\end{equation*}
The friction force is given by
\begin{equation*}
F = - mr \dom = - {5k \over 7r} mg
\end{equation*}
The condition \(|F| \lt \mu N\) imposes \(k/r \lt 7\mu/5\text{,}\) which is satisfied since the ratio \(k/r\) is expected to be much smaller than \(\mu\text{.}\)