Mechanical Actions

Skip to main content

\(\newcommand{\val}{Val\text{00E9}ry} \newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\R}{\mathbb R} \newcommand{\cA}{{\mathcal{A}}} \newcommand{\cB}{{\mathcal{B}}} \newcommand{\cC}{{\mathcal{C}}} \newcommand{\cD}{{\mathcal{D}}} \newcommand{\cE}{{\mathcal{E}}} \newcommand{\cF}{{\mathcal{F}}} \newcommand{\cG}{{\mathcal{G}}} \newcommand{\cH}{{\mathcal{H}}} \newcommand{\cI}{{\mathcal{I}}} \newcommand{\cJ}{{\mathcal{J}}} \newcommand{\cL}{{\mathcal{L}}} \newcommand{\cM}{{\mathcal{M}}} \newcommand{\Pow}{{\mathbb{P}}} \newcommand{\cP}{{\mathcal{P}}} \newcommand{\cR}{{\mathcal{R}}} \newcommand{\cS}{{\mathcal{S}}} \newcommand{\cT}{{\mathcal{T}}} \newcommand{\cU}{{\mathcal{U}}} \newcommand{\cV}{{\mathcal{V}}} \newcommand{\cW}{{\mathcal{W}}} \newcommand{\cX}{{\mathcal{X}}} \newcommand{\bze}{{\bf 0}} \newcommand{\bA}{{\bf A}} \newcommand{\ba}{{\bf a}} \newcommand{\bha}{{\bf \hat{a}}} \newcommand{\bB}{{\bf B}} \newcommand{\bob}{{\bf b}} \newcommand{\bhb}{{\bf \hat{b}}} \newcommand{\bC}{{\bf C}} \newcommand{\bc}{{\bf c}} \newcommand{\bhc}{{\bf \hat{c}}} \newcommand{\bD}{{\bf D}} \newcommand{\bod}{{\bf d}} \newcommand{\be}{{\bf \hat{e}}} \newcommand{\bef}{{\bf \hat{f}}} \newcommand{\bof}{{\bf f}} \newcommand{\force}{{\bf f}} \newcommand{\bF}{{\bf F}} \newcommand{\tbF}{\tilde{\bf F}} \newcommand{\bG}{{\bf G}} \newcommand{\bog}{{\bf g}} \newcommand{\bg}{{\bf g}} \newcommand{\bH}{{\bf H}} \newcommand{\bh}{{\bf h}} \newcommand{\bI}{{\bf I}} \newcommand{\bi}{{\boldsymbol{\hat{\imath}}}} \newcommand{\bj}{{\boldsymbol{\hat{\jmath}}}} \newcommand{\bk}{{\bf \hat{k}}} \newcommand{\bK}{{\bf \hat{K}}} \newcommand{\bL}{{\bf L}} \newcommand{\bl}{\mathbfit{l}} \newcommand{\bM}{{\bf M}} \newcommand{\bn}{{\bf \hat{n}}} \newcommand{\bq}{{\bf q}} \newcommand{\conjQ}{\overline{Q}} \newcommand{\conjP}{\bar{P}} \newcommand{\bp}{{\bf p}} \newcommand{\br}{{\bf r}} \newcommand{\bs}{{\bf s}} \newcommand{\bS}{{\bf S}} \newcommand{\bR}{{\bf R}} \newcommand{\bT}{{\bf T}} \newcommand{\bt}{{\bf \hat{t}}} \newcommand{\bu}{{\bf \hat{u}}} \newcommand{\buu}{{\bf {u}}} \newcommand{\bU}{{\bf U}} \newcommand{\vel}{{\bf v}} \newcommand{\bV}{{\bf V}} \newcommand{\bv}{{\bf \hat{v}}} \newcommand{\bvv}{{\bf {v}}} \newcommand{\vv}{{\bf v}^*} \newcommand{\bww}{{\bf {w}}} \newcommand{\pvel}{{\bf w}} \newcommand{\bW}{{\bf W}} \newcommand{\bw}{{\bf \hat{w}}} \newcommand{\bx}{{\bf \hat{x}}} \newcommand{\bxx}{{\bf x}} \newcommand{\bX}{{\bf X}} \newcommand{\bY}{{\bf Y}} \newcommand{\by}{{\bf \hat{y}}} \newcommand{\byy}{{\bf y}} \newcommand{\bz}{{\bf \hat{z}}} \newcommand{\bom}{\boldsymbol{\omega}} \newcommand{\bde}{\mathbf{\delta}} \newcommand{\bOm}{\boldsymbol{\Omega}} \newcommand{\bal}{\boldsymbol{\alpha}} \newcommand{\bomFE}{{\boldsymbol{\omega}}_{\cF/\cE}} \newcommand{\bomBA}{{\boldsymbol{\omega}}_{\cB/\cA}} \newcommand{\bGa}{\boldsymbol{\Gamma}} \newcommand{\btau}{\hat{\boldsymbol{\tau}}} \newcommand{\rot}{\boldsymbol{\tau}} \newcommand{\grad}{\boldsymbol{\nabla}} \newcommand{\iner}{{\cal I}_B} \newcommand{\inerG}{{\cal I}_G} \newcommand{\Earth}{\text{Earth}} \newcommand{\Arrow}{\mbox {$\longrightarrow$}} \newcommand{\half}{\frac{1}{2}} \newcommand{\al}{\alpha} \newcommand{\ep}{\epsilon} \newcommand{\ga}{\gamma} \newcommand{\te}{\theta} \newcommand{\la}{\lambda} \newcommand{\om}{\omega} \newcommand{\Om}{\Omega} \newcommand{\ro}{\rho} \newcommand{\Si}{\Sigma} \newcommand{\pSi}{{\partial \Sigma}} \newcommand{\bSi}{{\bar{\Sigma}}} \newcommand{\si}{\sigma} \newcommand{\dl}{\dot{l}} \newcommand{\ddl}{\ddot{l}} \newcommand{\dep}{\dot{\ep}} \newcommand{\ddep}{\ddot{\ep}} \newcommand{\ddbe}{\ddot{\beta}} \newcommand{\dbe}{\dot{\beta}} \newcommand{\dal}{\dot{\alpha}} \newcommand{\ddal}{\ddot{\alpha}} \newcommand{\ddga}{\ddot{\gamma}} \newcommand{\dphi}{\dot{\phi}} \newcommand{\ddphi}{\ddot{\phi}} \newcommand{\dpsi}{\dot{\psi}} \newcommand{\ddpsi}{\ddot{\psi}} \newcommand{\dte}{\dot{\te}} \newcommand{\ddte}{\ddot{\te}} \newcommand{\dom}{\dot{\om}} \newcommand{\dx}{\dot{x}} \newcommand{\ddx}{\ddot{x}} \newcommand{\dX}{\dot{X}} \newcommand{\ddX}{\ddot{X}} \newcommand{\dy}{\dot{y}} \newcommand{\ddy}{\ddot{y}} \newcommand{\dY}{\dot{Y}} \newcommand{\ddY}{\ddot{Y}} \newcommand{\dz}{\dot{z}} \newcommand{\dZ}{\dot{Z}} \newcommand{\ddz}{\ddot{z}} \newcommand{\ddZ}{\ddot{Z}} \newcommand{\Dp}{\dot{p}} \newcommand{\ddr}{\ddot{r}} \newcommand{\dr}{\dot{r}} \newcommand{\dq}{\dot{q}} \newcommand{\dQ}{\dot{Q}} \newcommand{\tq}{\tilde{q}} \newcommand{\ddq}{\ddot{q}} \newcommand{\dbq}{\dot{{\bf q}}} \newcommand{\ddbq}{\ddot{{\bf q}}} \newcommand{\dds}{\ddot{s}} \newcommand{\ds}{\dot{s}} \newcommand{\dro}{\dot{\ro}} \newcommand{\ddro}{\ddot{\ro}} \newcommand{\dv}{\dot{v}} \newcommand{\du}{\dot{u}} \newcommand{\bSi}{\overline{\Sigma}} \newcommand{\coB}{\overline{{\cal B}}} \newcommand{\kin}{\mathbb{K}} \newcommand{\qQ}{{\mathbb{Q}}} \newcommand{\pot}{{\mathbb{U}}} \newcommand{\hal}{{\mathbb{H}}} \newcommand{\lag}{{\mathbb{L}}} \newcommand{\gib}{{\mathbb{S}}} \newcommand{\energ}{{\mathbb{E}}} \newcommand{\danger}{\text{⚠}} \newcommand{\ddanger}{\text{⚠}} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \definecolor{fillinmathshade}{gray}{0.9} \newcommand{\fillinmath}[1]{\mathchoice{\colorbox{fillinmathshade}{$\displaystyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\textstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptscriptstyle\phantom{\,#1\,}$}}} \)

Chapter 10 Mechanical Actions

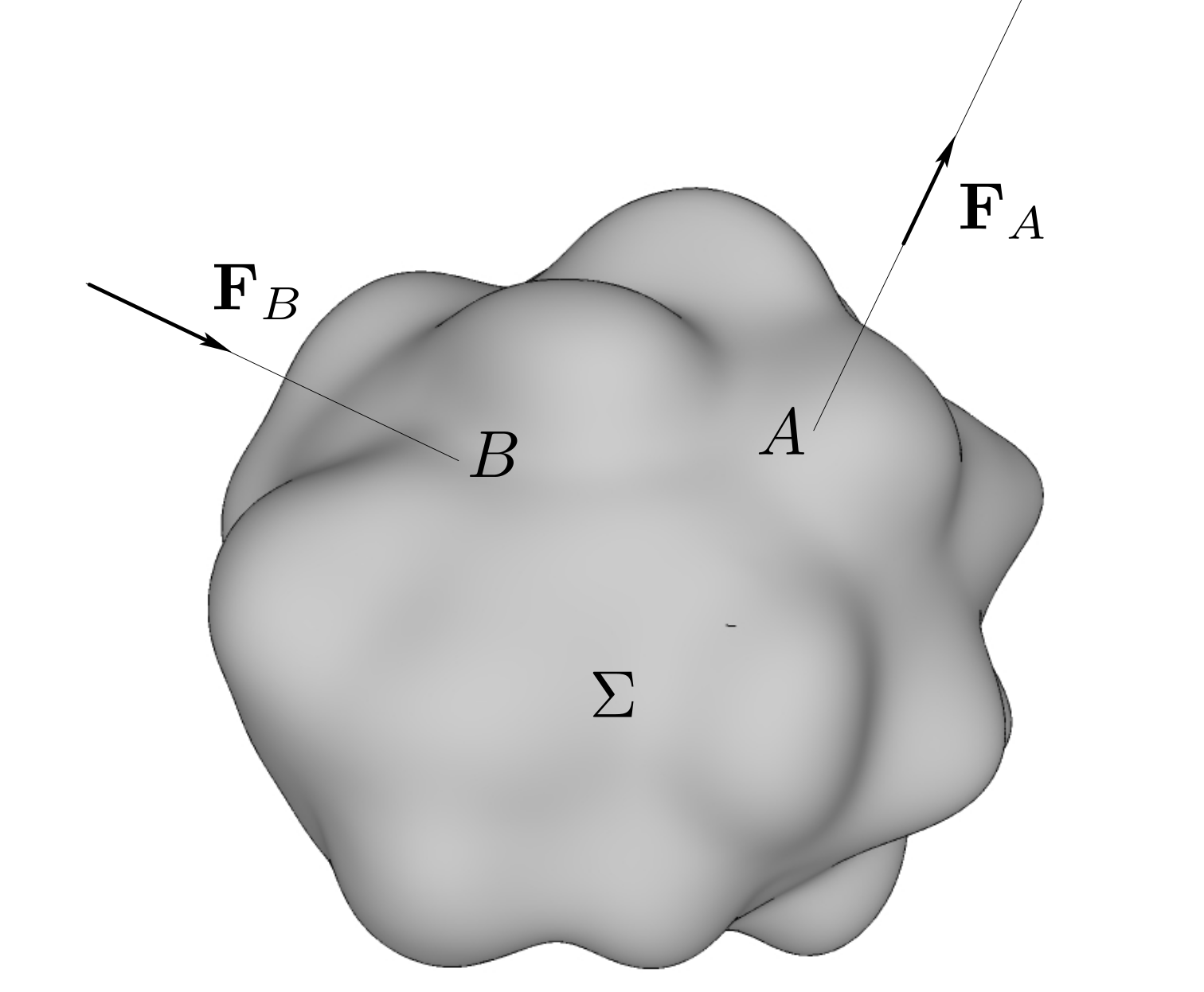
In this chapter, we seek to model the mechanical actions exerted on a material system \(\Sigma\text{.}\) We define a mechanical action as any cause capable of either maintaining a material system in equilibrium, or of modifying its motion or shape. On the simplest level, recall that the action of a force \(\bF_A\) exerted on a system \(\Sigma\) is properly defined by indicating both the value of vector \(\bF_A\) and its line of action (or simply a point on this line of action): hence this mechanical action is defined by the bound vector \((A, \bF_A)\) or in the language of screws by the slider denoted as

\begin{equation*} \left\{ \begin{array}{c} \bF_A \\ \bze \end{array} \right\}_A \end{equation*}

Screws are useful tools to account for the sum of discrete forces, or for the sum of forces distributed over \(\Sigma\) (or over a subset of \(\Si\)). For instance, the action of force \(\bF_A\) acting through point \(A\) and force \(\bF_B\) acting through point \(B\) results in the screw (see Figure 10.0.1)

\begin{equation*} \left\{ \begin{array}{c} \bF_A \\ \bze \end{array} \right\}_A + \left\{ \begin{array}{c} \bF_B \\ \bze \end{array} \right\}_B = \left\{ \begin{array}{c} \bF_A + \bF_B \\ \bF_A \times\br_{AQ} +\bF_B \times\br_{BQ} \end{array} \right\}_Q \end{equation*}

More generally, in the case of distributed forces, we consider two types of interactions between material systems \(\Sigma_1\) and \(\Sigma_2\text{:}\) action at-a-distance (such as gravitational actions) exerted at every point within the volume of each systems, and contact actions exerted on all or part of their boundary. From a local description of elementary forces modeled as bound vectors (or sliders) acting on infinitesimal elements of volume or surface of \(\Sigma_2\text{,}\) we obtain a global description of the action of \(\Sigma_1\) on \(\Sigma_2\) in term of a screw called action screw, and denoted as \(\{ \cA_{\Sigma_1 \to \Sigma_2} \}\text{.}\) The global effect of all mechanical actions exerted on a material system will be defined in terms of the total external action screw.

Figure 10.0.1.