1.
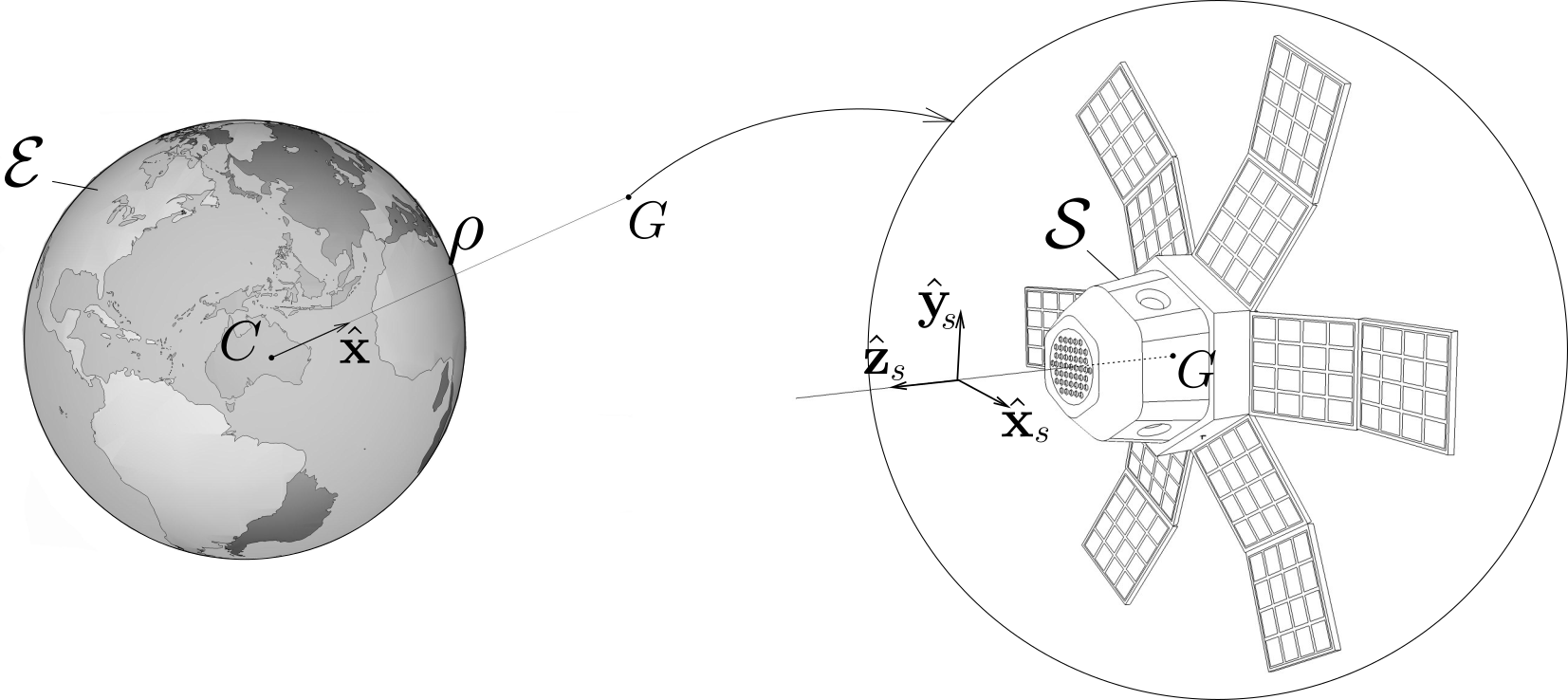
Planets assume the shape of oblate spheroids due to their rotation. This shape is characterized by a flattening ratio \(f = (R_E - R_P)/R_E\text{,}\) defined as the ratio of the equatorial-polar radius difference \((R_E-R_P)\) to the equatorial radius \(R_E\text{.}\) The goal of this problem is to derive an expression for the gravitational field \(\bG_\Sigma\) created by such a body \(\Sigma\) of mass center \(O\text{,}\) mass \(M\text{,}\) equatorial plane \(Oxy\text{,}\) and polar axis \(Oz\text{.}\)

- With reference to the figure, show that the gravitational field \(\bG_\Sigma (P)\) at a point \(P\) of position \(\br\equiv \br_{OP} = r\be_r\) is given by\begin{equation*} \bG_\Sigma (P) = -{G \over r^2} \be_r \int_\Sigma \left[ 1 - \frac{3}{2r^2} (\bs^2 -5 (\bs\cdot\be_r)^2 ) \right] \, dm + {3G \over r^4} \int_{\Sigma} (\bs\cdot\be_r) \bs \, dm \end{equation*}assuming that the distance \(r \equiv | \br_{OP}|\) from \(P\) to \(O\) is much larger than the distance \(|\bs|\) from any point \(Q\) of \(\Sigma\) to \(O\) (use the expansion \((1+x)^{-3/2} = 1 -3x/2 +15x^2 /8 + \cdots\))
- Show that \(\bG_\Sigma\) is given by the expression\begin{equation*} \bG_\Sigma (P) = - {G M \over r^2} \be_r + {3G \over 2r^4} (A-C) \left[ (1-3\sin^2 \phi)\be_r + 2 \sin\phi\cos\phi \be_\phi \right] \end{equation*}in terms of the coordinates \((r, \phi)\) of point \(P\text{,}\) and of the equatorial and polar moments of inertia \(A = I_{Ox} = I_{Oy}\) and \(C = I_{Oz}\text{.}\)
- Deduce that the gravitational field can be expressed in terms of potential \(\pot\text{,}\) that is\begin{equation*} \bG_\Sigma (P) = -\nabla \pot, \qquad \pot= - {G M \over r} + {G \over 2r^3} (C-A) (3\sin^2\phi -1) \end{equation*}with \(\nabla = - \be_r \partial / \partial r - \be_\phi \partial / r\partial\phi\text{.}\) Assuming that the free surface of \(\Sigma\) is a surface of equipotential, show that the flattening ratio \(f\) takes the expression\begin{equation*} f = \frac{3}{2} \frac{(C-A)}{MR_E^2} \end{equation*}(The value of \(f\) can range from 1/300 for Earth to 1/10 for Saturn).