Advanced Engineering Dynamics

Subsection 7.3.1 Assumptions

Subsection 7.3.2 The slip velocity of a rigid body

1. It can be related to the motion of point \(I\) relative to \(\cB_{1}\) and \(\cB_{2}\) by application of formula (6.2.1):

   \begin{equation} \vel_{I \in 2 / 1 }= \vel_{I / 1 } - \vel_{I / 2 }\tag{7.3.3} \end{equation}

   where

   \begin{equation*} \vel_{I / 1 } = \left( {d\br_{O_1 I} \over dt} \right)_1, \qquad \vel_{I / 2 } = \left( {d\br_{O_2 I} \over dt} \right)_2 \end{equation*}

   As \(\cB_2\) moves relative to \(\cB_1\text{,}\) contact point \(I\) describes the trajectory \(\cC_1\) relative to \(\cB_1\) inscribed on the surface of \(\cB_1\) and the trajectory \(\cC_2\) relative to \(\cB_2\) inscribed on the surface of \(\cB_2\text{.}\) Velocity \(\vel_{I /1}\) is tangent to curve \(\cC_1\text{,}\) while velocity \(\vel_{I /2}\) is tangent to curve \(\cC_2\text{.}\) Since both vectors \(\vel_{I /1}\) and \(\vel_{I /2}\) must necessarily lie in plane \(\Pi\text{,}\) a consequence of equation (7.3.3) is that the slip velocity also lies in tangential plane \(\Pi\text{,}\) as long as contact is maintained. This provides a justification of condition \(\vel_{I \in 2 / 1 } \cdot \bn_{12} = 0\) of equation (7.3.2).
2. It can be related to the motion of \(\cB_{1}\) and \(\cB_{2}\) relative to a referential \(\cB_0\) according to equation (7.3.1):

   \begin{equation} \vel_{I \in 2 / 1} = \vel_{I \in 2 /0}- \vel_{I \in 1 /0}\tag{7.3.4} \end{equation}

   where

   \begin{equation*} \vel_{I \in i /0} = \vel_{O_i / 0} + \bom_{i / 0} \times \br_{O_i I}, \qquad i=1,2 \end{equation*}

   is the velocity relative to \(\cB_0\) of the point of body \(\cB_i\) coinciding with contact point \(I\text{.}\) Equation (7.3.4) is especially useful when the motions of \(\cB_{1}\) and \(\cB_{2}\) are parametrized relative to a referential \(\cB_0\text{.}\)

Subsection 7.3.3 Pivoting and Rolling of a Rigid Body

Subsection 7.3.4 The Axodes of a Rigid Body Motion

Subsection 7.3.5 Examples

Example 7.3.9. Rolling Motion of a Cylindrical Tube.

A cylinder \(\cB_1 (C, \bx_1 , \by_1 ,\bz_0)\) whose cross-section is not necessarily circular is in rolling motion on a right circular cylindrical support of a referential \(\cB_0 (O, \bx_0 , \by_0 , \bz_0)\text{.}\) See Figure 7.3.10.

The boundary of \(\cB_1\) is defined as a closed curve defined as the set of points \(Q\) satisfying

\begin{equation*} \br_{CQ} (s) = f(s) \bx_1 + g(s)\by_1 \end{equation*}

where the given functions \(f\) and \(g\) are \(2\pi\)-periodic in the parameter \(s\text{.}\) The position of \(\cB_1\) is defined by

1. the angle \(\phi = (\bx_0 , \bx_1) = (\by_0 , \by_1)\) defining the orientation of basis \((\bx_1 , \by_1 , \bz_1 = \bz_0 )\text{,}\)
2. the angle \(\theta = (\bx_0 , \bx_2) = (\by_0 , \by_2)\) defining the position of contact point \(I\text{:}\) \(\br_{OI} = R \bx_2\text{.}\)

1. Find the slip velocity \(\vel_{I\in 1/0}\) of body \(\cB_1\) relative to \(\cB_0\text{.}\) Deduce a geometric condition which guarantees contact at \(I\text{.}\) Then find velocity \(\vel_{C/0}\text{.}\)
2. Assume that \(\cB_1\) rolls without slipping on \(\cB_0\text{.}\) Show that the no-slip condition can be reduced to a holonomic constraint equation. Then consider the case of (i) a circular cylinder \((f,g)= (r\cos s, r\sin s)\text{,}\) and (ii) of an elliptic cylinder \((f,g)= (a\cos s, b\sin s)\text{.}\)

Solution.

1. The contact velocity \(\vel_{I\in 1/0}\) can be found as follows

   \begin{equation*} \vel_{I\in 1/0} = \vel_{I/0}- \vel_{I/1} \end{equation*}

   where velocity \(\vel_{I/0}\) found as \((d\br_{OI} /dt)_0\)

   \begin{equation*} \vel_{I/0}= \left( \frac{ d (R \bx_2)}{dt} \right)_0 = R \dte \by_2 \end{equation*}

   Likewise, velocity \(\vel_{I/1}\) is found as the time-derivative of \(\br_{CI}\) relative to body \(\cB_1\text{.}\) Since the trajectory of \(I\) relative to \(\cB_1\) lies on the boundary of \(\cB_1\text{,}\) we can write \(\br_{CI} = f(s) \bx_1 + g(s)\by_1\) where scalar \(s= s(t)\) parametrizes the position of \(I\text{.}\) This leads to

   \begin{equation*} \vel_{I/1}= \left( \frac{d}{dt} (f(s) \bx_1 + g(s)\by_1) \right)_1 = \ds (f' \bx_1 + g' \by_1) \end{equation*}

   with \(f' = df/ds\text{,}\) \(g'= dg/ds\text{.}\) This gives

   \begin{equation*} \vel_{I\in 1/0} = R \dte \by_2 - \ds (f' \bx_1 + g' \by_1) \end{equation*}
   The slip-velocity \(\vel_{I\in 1/0}\) must be tangent at \(I\) with the contact line for the contact to be realized. Hence, we must impose \(\vel_{I\in 1/0} \cdot \bx_2 = 0\text{.}\) This gives the equation

   \begin{equation*} - \ds (f' \bx_1 + g' \by_1)\cdot \bx_2 = -\ds (f' \cos(\theta -\phi) + g' \sin(\theta -\phi) ) =0 \end{equation*}

   which can be recast as

   \begin{equation*} \tan(\theta -\phi) = G(s) = - \frac{f'(s)}{g'(s)} \qquad (1) \end{equation*}

   This relationship enables the determination of the position of \(I\) (and hence of \(C\)) as a function of angle \((\theta - \phi)\text{.}\) From equation

   \begin{equation*} \br_{OC} = \br_{OI}+ \br_{IC} = R\bx_2 -f \bx_1 -g \by_1 \end{equation*}

   we obtain the velocity of \(C\text{:}\)

   \begin{equation*} \vel_{C/0} = R \dte \by_2 - \ds (f' \bx_1 +g' \by_1) + \dphi (f \by_1 - g \bx_1) \end{equation*}

   with \(G'(s) \ds = (\dte - \dphi)/\cos^2 (\theta - \phi)\) by differentiation of (1).
2. The no-slip condition is imposed by setting \(\vel_{I\in 1/0} = \bze\text{:}\)

   \begin{equation*} R \dte = \ds (- f'\sin(\theta -\phi) + g'\cos(\theta -\phi) ) \end{equation*}

   This equation imposes a relationship between \(\phi\) and \(\theta\text{.}\) This is an integrable non-holonomic constraint equation: by using (1) we can express \(\theta\) versus \(s\)

   \begin{equation*} R(\te -\te_0) = \int_{s_0}^s (f'^2 + g'^2)^{1/2} ds \qquad(2) \end{equation*}

   \(\te_0\) and \(s_0\) are constants of integration. For the circular cylinder, we find from (2) \(R\dte = r \ds\) and from (1) \(\tan(\te-\phi) = \tan s\) or \(\dte - \dphi = \ds\) leading to

   \begin{equation*} \phi - \phi_0 = (1+\frac{R}{r}) (\te -\te_0 ) \end{equation*}

   For the elliptic cylinder, (2) gives \(\te\) versus \(s\)

   \begin{equation*} R(\te -\te_0) = \int_{s_0}^s (a^2 \sin^2 s + b^2 \cos^2 s)^{1/2} ds \end{equation*}

   and (1) gives \(\phi\) versus \(s\text{.}\) We can also find a quadrature formula giving \(\te\) versus \(\phi\) by eliminating \(s\text{:}\)

   \begin{equation*} R(\te -\te_0) = \int_{\psi_0}^\psi \frac{a^2b^2}{(a^2 \cos^2 u + b^2 \sin^2 u)^{3/2}} du \end{equation*}

   by defining \(\psi = \te-\phi\) and \(\psi_0 = \te_0-\phi_0\text{.}\) In both cases, we recognize that equation (2) expresses the equality of arc length of the two curves (the centrodes) described by \(I\) on the boundary of \(\cB_0\) and \(\cB_1\text{.}\)

Example 7.3.11. Rolling and pivoting of a disk on a horizontal support.

A disk \(\cB_1\) of center \(C\) and radius \(R\) is constrained to roll, pivot and slip about contact point \(I\) relative to horizontal plane \((O, \bx_0 , \by_0)\) of a referential \(\cB_0\text{.}\) Its position is defined by the coordinates \((x_I,y_I)\) of contact point \(I\) and by the three Euler angles \((\psi , \te , \phi)\) as defined in Figure 7.3.12.

1. Determine the kinematic screw of \(\cB_1\text{.}\) Find the pivoting and rolling components of the angular velocity of \(\cB_1\text{.}\) Find its angular acceleration.
2. After finding the slip velocity \(\vel_{I\in 1 /0}\text{,}\) determine the kinematic constraint equations which express the no-slip condition of \(\cB_1\) relative to \(\cB_0\text{.}\) Can \(\cB_1\) roll without slipping and pivoting?

Solution.

1. The parametrization of the position of disk \(\cB_1 (C, \bx_1, \by_1,\bz_1)\) relative to \(\cB_0 (O, \bx_0,\by_0,\bz_0)\) is done with the set of coordinates \((x_I, y_I, \psi, \te, \phi)\) defined as follows:
   1. \((x_I,\,y_I )\) are the Cartesian coordinates of contact point \(I\) on the axes \((O,\bx_0)\) and \((O,\by_0)\text{.}\)
   2. angle \(\psi\) defines the orientation of the line \((I, \, \bx_2)\) tangent at the point of contact \(I\) to the rim of the disk: \(\psi = (\bx_0,\bx_2)\text{.}\) This leads to the transformation

      \begin{equation*} (\bx_0 ,\by_0 , \bz_0) \xrightarrow{\cR_{\psi, \bz_0}} (\bx_2 ,\by_2 ,\bz_2 = \bz_0) \end{equation*}
   3. angle \(\te\) defines the orientation of the normal \((I, \bz_3)\) to disk \(\cB_1\text{:}\) \(\te = (\bz_0,\bz_3)\text{.}\) Then, we define \(\by_3 = \bz_3 \times \bx_2\) such that \(\br_{IC} = R \by_3\text{.}\) This leads to the transformation

      \begin{equation*} (\bx_2 ,\by_2 , \bz_0) \xrightarrow{\cR_{\te, \bx_2}} (\bx_3 = \bx_2 ,\by_3 , \bz_3) \end{equation*}
   4. the basis \((\bx_1 , \by_1, \bz_1 = \bz_3)\) attached to \(\cB_1\) is obtained from basis \((\bx_3 = \bx_2 , \by_3 , \bz_3)\) by a rotation of angle \(\phi = (\bx_2,\bx_1) = (\by_3,\by_2)\) about \(\bz_3\text{:}\)

      \begin{equation*} (\bx_2 ,\by_3 , \bz_3)\xrightarrow{\cR_{\phi, \bz_3}} (\bx_1 , \by_1, \bz_1 = \bz_3) \end{equation*}
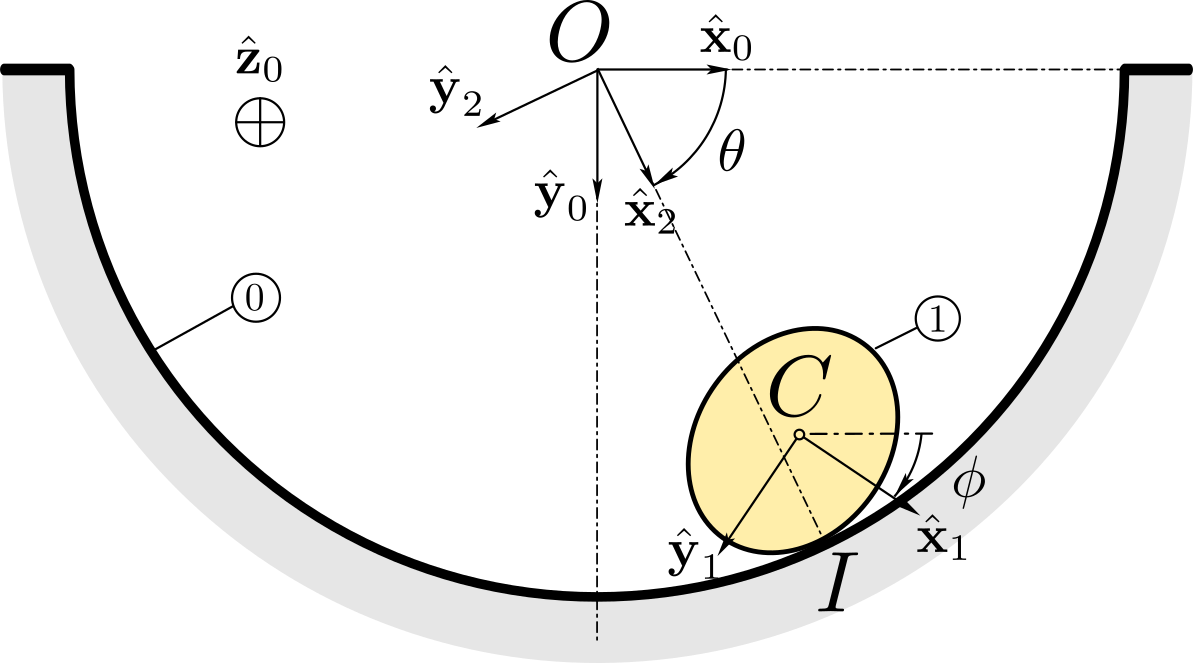
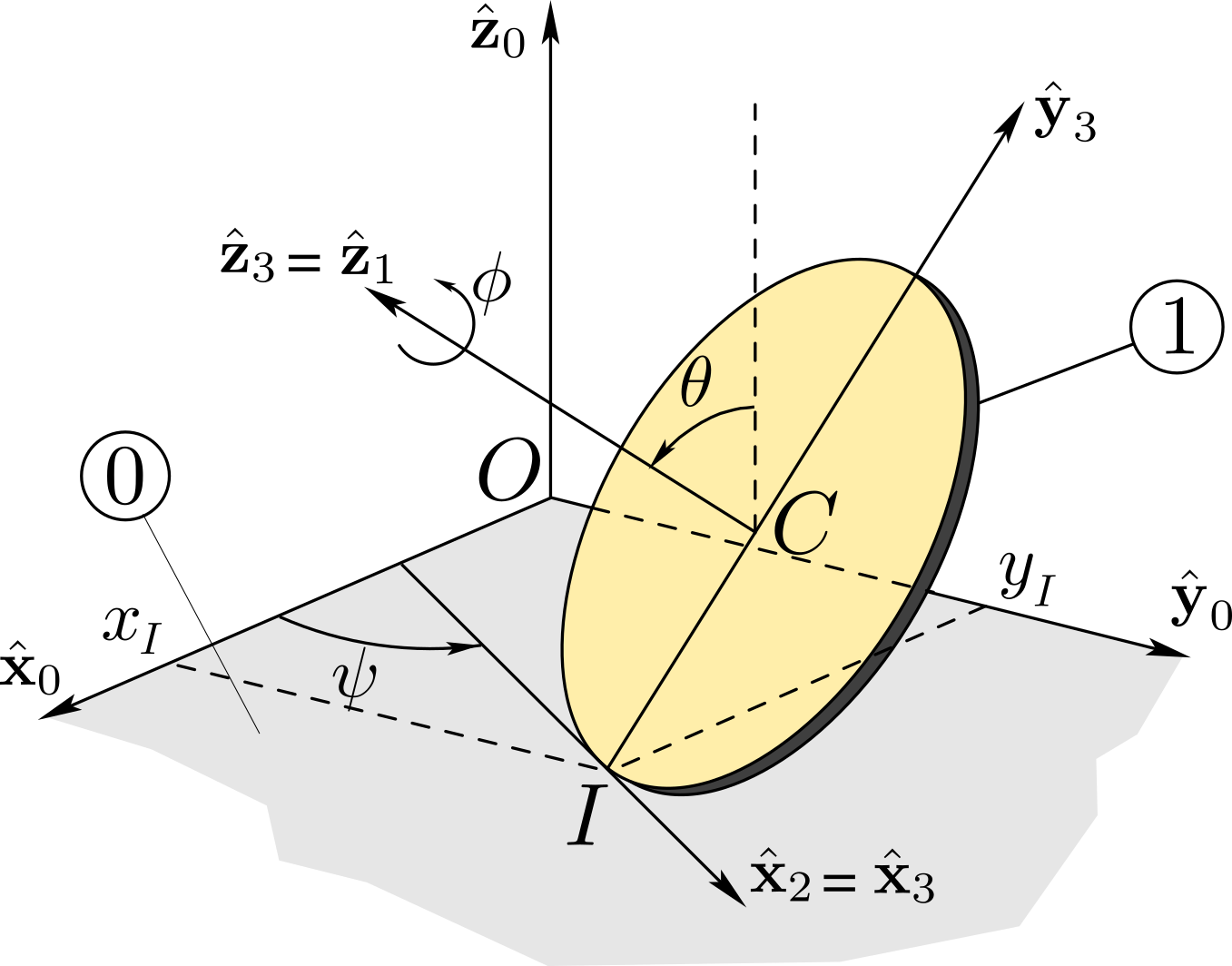
   With this parametrization, we find the angular velocity of the disk

   \begin{equation*} \bom_{1/0} = \bom_{1/3} +\bom_{3/2}+ \bom_{2/0}=\dphi \bz_3+\dte \bx_2+ \dpsi \bz_0\text{.} \end{equation*}

   To find the pivoting component of \(\bom_{1/0}\text{,}\) we project \(\bom_{1/0}\) on the unit normal \(\bz_0\text{:}\)

   \begin{equation*} \bom^{n}_{1/0} = ( \bom_{1/0} \cdot \bz_0 ) \bz_0 = [(\dpsi \bz_0 + \dte \bx_2+ \dphi \bz_3) \cdot \bz_0 ] \bz_0 \end{equation*}

   or

   \begin{equation*} \bom^{n}_{1/0} = (\dpsi + \dphi\cos\te ) \bz_0 \end{equation*}

   The rolling component is then given by \(\bom_{1/0}^{t} = \bom_{1/0} - \bom_{1/0}^{n}\)

   \begin{equation*} \bom^{t}_{1/0} = \dte \bx_2 - \dphi \sin\te \by_2 \end{equation*}

   The angular acceleration of \(\cB_1\) relative to \(\cB_0\) can be found as:

   \begin{equation*} \bal_{1/0} = \ddphi \bz_3 + \ddte \bx_2 + \ddpsi \bz_0 + \dphi (\dte\bx_2+\dpsi\bz_0)\times \bz_3 + \dte \dpsi \by_2 \end{equation*}

   leading to, on basis \((\bx_3, \by_3, \bz_3)\)

   \begin{align*} \bal_{1/0} = (\ddte +\dpsi\dphi\sin\te)\bx_3 \amp + (\ddpsi \sin\te -\dte\dphi +\dpsi\dte \cos\te)\by_3\\ \amp \quad + (\ddphi + \ddpsi \cos\te - \dpsi\dte \sin\te)\bz_3 \end{align*}

   To write the kinematic screw \(\{ {\cal V} _{1/0 } \}\) of \(\cB_1\text{,}\) we need to find the velocity of center \(C\) by differentiating the position vector \(\br_{OC} = x_I \bx_0 + y_I \by_0 + R \by_3\text{:}\)

   \begin{align*} \vel_{C / 0} \amp = \dx_I \bx_0 + \dy_I \by_0 + R (\dte\bx_2+\dpsi\bz_0)\times \by_3\\ \amp = \dx_I \bx_0 + \dy_I \by_0 +R (\dte \bz_3 -\dpsi\cos\te\bx_3) \end{align*}

   This leads to the expression

   \begin{equation*} \{ {\cal V} _{1/0 } \} = \begin{Bmatrix} \dphi \bz_3+\dte \bx_2+ \dpsi \bz_0 \\ \\ \dx_I \bx_0 + \dy_I \by_0 + R (\dte \bz_3 -\dpsi\cos\te\bx_3) \end{Bmatrix}_C \end{equation*}
2. To find slip-velocity at \(I\text{,}\) that is, the velocity of the point of \(\cB_1\) coinciding with \(I\text{,}\) we use the kinematic screw formula:

   \begin{equation*} \vel_{I \in 1/0} = \vel_{C\in 1/0} + \bom _{1/0 } \times \br_{CI} = \vel_{C\in 1/0} + R (\dphi \bx_3 - \dte \bz_3 +\dpsi\cos\te\bx_3) \end{equation*}

   This gives, after simplifications,

   \begin{equation*} \vel_{I \in 1/0} = \dx_I \bx_0 + \dy_I \by_0 + R \dphi \bx_3 \qquad(1) \end{equation*}

   Note that the condition \(\vel_{I\in 1/0} \cdot \bz_0 =0\) is satisfied since the parametrization in terms of \((x_I,y_I,\psi,\theta, \phi)\) takes into account the condition of contact at \(I\text{.}\) The expression of the slip-velocity can be used to define the kinematic screw of \(\cB_1\text{:}\)

   \begin{equation*} \{ {\cal V}_{ 1/0 } \} = \begin{Bmatrix} \dphi \bz_3+\dte \bx_2+ \dpsi \bz_0 \\ \\ \dx_I \bx_0 + \dy_I \by_0 + R\dphi \bx_3 \end{Bmatrix}_I \end{equation*}

   If \(\cB_1\) rolls and pivots without slipping on \(\cB_0\text{,}\) then \(\vel_{I \in 1/0}= {\bf 0}\text{:}\) we project equation (1) on \((\bx_0, \by_0)\) to obtain the following two non-holonomic constraints equations

   \begin{equation*} \begin{array}{ll} \dx_I \amp = -R \dphi \cos\psi \\ \dy_I \amp = -R \dphi \sin\psi \end{array} \end{equation*}

   These equations are non-integrable. For \(\cB_1\) to roll without slipping and pivoting, a third non-holonomic equation must be imposed:

   \begin{equation*} \dpsi + \dphi\cos\te = 0 \end{equation*}

Remark 7.3.13.

We could have found \(\vel_{I \in 1/0}\) as the difference \(\vel_{I/0} -\vel_{I/1}\) with

\begin{equation*} \vel_{I/0} = (d \br_{OI} /dt)_0 = \dx_I \bx_0 + \dy_I \by_0 \end{equation*}

and

\begin{equation*} \vel_{I/1} = (d \br_{CI} /dt)_1 = -R \bom_{3/1}\times \by_3 = R \dphi \bz_3 \times \by_3 = -R \dphi \bx_3 \end{equation*}

We recover the same expression.

Example 7.3.14.

Figure 7.3.15 shows two rigid bodies \(\cB_1\) and \(\cB_2\) in relative motion in a referential \(\cB_0\) of origin \(O\) and basis \((\bx_0 , \by_0 , \bz_0 )\text{.}\) Body \(\cB_1\) is a truncated cone (of half-angle \(\alpha\text{.}\) connected to \(\cB_0\) by a pivot of axis \((A , \bu)\) (the axis of the cone) whose orientation in \(\cB_0\) is defined by angle \(\alpha\text{.}\) The angular velocity of body \(\cB_1\) is \(\bom_{1/0} = \omega_1 \bu\text{.}\) Body \(\cB_2\) is a circular platform mounted on a pivot of axis \((O, \bz_0)\text{:}\) its angular velocity is \(\bom_{2/0} = \omega_2 \bz_0\text{.}\) The two bodies are in contact along the line segment \(IJ\text{.}\) Figure 7.3.15 represents the plane containing both axes \((A, \bu)\) and \((O, \bz_0)\text{.}\) Denote by \(a\) the distance \(|OA|\text{.}\)

1. Find the angular velocity \(\bom_{2/1}\) of body \(\cB_2\) relative to body \(\cB_1\text{.}\) Decompose \(\bom_{2/1}\) into rolling and pivoting components.
2. Express the kinematic screw \(\{ {\cal V}_{2/1} \}\) at a point of your choice.
3. Find the velocity \(\vel_{Q \in 2/1}\) of any point \(Q\) of the contact line \(OA\text{.}\) Deduce that the instantaneous screw axis \(\Delta_{2/1}\) passes through two points in the plane of the figure. What is the corresponding velocity of points of the screw axis? Describe the two axodes generated by the motion of \(\Delta_{2/1}\) relative to \(\cB_1\) and to \(\cB_2\text{,}\) then characterize the motion of \(\cB_2\) relative to \(\cB_1\) in terms of the relative motion of the axodes.

Solution.

1. We obtain \(\bom_{2/1}\) by taking the difference between \(\bom_{2/0}\) and \(\bom_{1/0}\text{:}\)

   \begin{equation*} \bom_{2/1} = \bom_{2/0}- \bom_{1/0} = \om_2 \bz_0 - \om_1 \bu = (\om_2 + \om_1 \sin\alpha) \bz_0 - \om_1 \cos\alpha \bx_0 \end{equation*}

   Since the two surfaces in contact (along line \(IJ\)) have a common normal along \(\bz_0\text{,}\) the pivoting component of \(\bom_{2/1}\) is \((\om_2 + \om_1 \sin\alpha) \bz_0\) and the rolling component is \(- \om_1 \cos\alpha \bx_0\text{.}\)
2. We first define \(\by_0 = \bz_0 \times \bx_0\text{.}\) We obtain kinematic screw \(\{ \cV_{2/1} \}\) as the difference between \(\{ \cV_{2/0} \}\) and \(\{ \cV_{1/0} \}\text{:}\)

   \begin{equation*} \{ \cV_{2/1} \} = \{ \cV_{2/0} \} - \{ \cV_{1/0} \} \end{equation*}

   Since the joint between \(\cB_1\) and \(\cB_0\) is a pivot of axis \((A, \bu)\text{,}\) we have:

   \begin{equation*} \{ \cV_{1/0} \} = \begin{Bmatrix} \om_1 \bu \\ \\ \bze \end{Bmatrix}_{A} \end{equation*}

   Similarly, the joint between \(\cB_2\) and \(\cB_0\) is a pivot of axis \((O, \bz_0)\text{:}\)

   \begin{equation*} \{ \cV_{2/0} \} = \begin{Bmatrix} \om_2 \bz_0 \\ \\ \bze \end{Bmatrix}_{O} \end{equation*}

   This leads to

   \begin{equation*} \{ \cV_{2/1} \} = \begin{Bmatrix} \om_2 \bz_0 \\ \\ \bze \end{Bmatrix}_{O} - \begin{Bmatrix} \om_1 \bu \\ \\ \bze \end{Bmatrix}_{A} = \begin{Bmatrix} \om_2 \bz_0 - \om_1 \bu \\ \\ -a \om_1 \sin\alpha \by_0 \end{Bmatrix}_{O} \end{equation*}

   where we have used \(\vel_{O\in 1/0}= \om_1 \bu \times \br_{AO} = - \om_1 \bu \times a \bx_0 = a \om_1 \sin\alpha \by_0\text{.}\)
3. First, we define the position of an arbitrary point on line OA as \(\br_{OQ} = \lambda \bx_0\) (\(\lambda\) is arbitrary scalar). We find \(\vel_{Q\in 2/1}\) by using the kinematic screw found in b):

   \begin{equation*} \vel_{Q\in 2/1} = \vel_{O\in 2/1}+ \bom_{2/1} \times \br_{OQ} = -a \om_1 \sin\alpha \by_0 + (\om_2 \bz_0 - \om_1 \bu) \times \lambda \bx_0 \end{equation*}

   leading to

   \begin{equation*} \vel_{Q\in 2/1} = [-a \om_1 \sin\alpha + \lambda (\om_2 + \om_1 \sin\alpha) ]\by_0 \end{equation*}

   Note the direction of \(\vel_{Q\in 2/1}\text{:}\) it has no component on \(\bz_0\text{,}\) as expected. We also note that \(\vel_{Q\in 2/1}\) has a non zero value for all points \(Q\) of line \(OA\) except if scalar \(\lambda\) takes the value

   \begin{equation*} \lambda_* = a \frac{\om_1 \sin\alpha}{\om_2 + \om_1 \sin\alpha } \end{equation*}

   We call \(Q_*\) the corresponding point: \(\vel_{Q_* \in 2/1} = \bze\) (this point lies between \(O\) and \(A\) if scalars \(\om_1\) and \(\om_2\) are both positive). The existence of point \(Q_*\) indicates that screw axis \(\Delta_{2/1}\) is an instantaneous axis of rotation since it passes through \(Q_*\text{.}\) Note that the corresponding pitch is necessarily zero. Another point of interest is point \(B\) defined as the intersection of the rotation axes \((A, \bu)\) and \((O, \bz_0)\text{:}\) since \(B\) belongs to both axes, we have

   \begin{equation*} \vel_{B\in 2/1} = \vel_{B\in 2/0} - \vel_{B\in 1/0} = \bze \end{equation*}

   Hence, point \(B\) must also belong to axis \(\Delta_{2/1}\text{:}\) we conclude that \(\Delta_{2/1}\) is the line \(BQ_*\text{.}\) This axis is fixed relative to referential \verb=0=. Relative to body \(\cB_2\text{,}\) it generates a cone of axis \((B, \bz_0)\) and apex \(B\text{.}\) Similarly, \(\Delta_{2/1}\) viewed from body \(\cB_1\) generates a cone of axis \((B, \bu)\) and apex \(B\text{.}\) The motion body \(\cB_2\) relative to body \(\cB_1\) (as far as velocities are concerned) is then equivalent to the motion of a cone of \(\cB_1\) rolling without slipping on a cone of \(\cB_2\text{.}\) See Figure 7.3.16 for a sketch of these two axodes.