Gyroscope: Definition

Skip to main content

\(\newcommand{\val}{Val\text{00E9}ry} \newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\R}{\mathbb R} \newcommand{\cA}{{\mathcal{A}}} \newcommand{\cB}{{\mathcal{B}}} \newcommand{\cC}{{\mathcal{C}}} \newcommand{\cD}{{\mathcal{D}}} \newcommand{\cE}{{\mathcal{E}}} \newcommand{\cF}{{\mathcal{F}}} \newcommand{\cG}{{\mathcal{G}}} \newcommand{\cH}{{\mathcal{H}}} \newcommand{\cI}{{\mathcal{I}}} \newcommand{\cJ}{{\mathcal{J}}} \newcommand{\cL}{{\mathcal{L}}} \newcommand{\cM}{{\mathcal{M}}} \newcommand{\Pow}{{\mathbb{P}}} \newcommand{\cP}{{\mathcal{P}}} \newcommand{\cR}{{\mathcal{R}}} \newcommand{\cS}{{\mathcal{S}}} \newcommand{\cT}{{\mathcal{T}}} \newcommand{\cU}{{\mathcal{U}}} \newcommand{\cV}{{\mathcal{V}}} \newcommand{\cW}{{\mathcal{W}}} \newcommand{\cX}{{\mathcal{X}}} \newcommand{\bze}{{\bf 0}} \newcommand{\bA}{{\bf A}} \newcommand{\ba}{{\bf a}} \newcommand{\bha}{{\bf \hat{a}}} \newcommand{\bB}{{\bf B}} \newcommand{\bob}{{\bf b}} \newcommand{\bhb}{{\bf \hat{b}}} \newcommand{\bC}{{\bf C}} \newcommand{\bc}{{\bf c}} \newcommand{\bhc}{{\bf \hat{c}}} \newcommand{\bD}{{\bf D}} \newcommand{\bod}{{\bf d}} \newcommand{\be}{{\bf \hat{e}}} \newcommand{\bef}{{\bf \hat{f}}} \newcommand{\bof}{{\bf f}} \newcommand{\force}{{\bf f}} \newcommand{\bF}{{\bf F}} \newcommand{\tbF}{\tilde{\bf F}} \newcommand{\bG}{{\bf G}} \newcommand{\bog}{{\bf g}} \newcommand{\bg}{{\bf g}} \newcommand{\bH}{{\bf H}} \newcommand{\bh}{{\bf h}} \newcommand{\bI}{{\bf I}} \newcommand{\bi}{{\boldsymbol{\hat{\imath}}}} \newcommand{\bj}{{\boldsymbol{\hat{\jmath}}}} \newcommand{\bk}{{\bf \hat{k}}} \newcommand{\bK}{{\bf \hat{K}}} \newcommand{\bL}{{\bf L}} \newcommand{\bl}{\mathbfit{l}} \newcommand{\bM}{{\bf M}} \newcommand{\bn}{{\bf \hat{n}}} \newcommand{\bq}{{\bf q}} \newcommand{\conjQ}{\overline{Q}} \newcommand{\conjP}{\bar{P}} \newcommand{\bp}{{\bf p}} \newcommand{\br}{{\bf r}} \newcommand{\bs}{{\bf s}} \newcommand{\bS}{{\bf S}} \newcommand{\bR}{{\bf R}} \newcommand{\bT}{{\bf T}} \newcommand{\bt}{{\bf \hat{t}}} \newcommand{\bu}{{\bf \hat{u}}} \newcommand{\buu}{{\bf {u}}} \newcommand{\bU}{{\bf U}} \newcommand{\vel}{{\bf v}} \newcommand{\bV}{{\bf V}} \newcommand{\bv}{{\bf \hat{v}}} \newcommand{\bvv}{{\bf {v}}} \newcommand{\vv}{{\bf v}^*} \newcommand{\bww}{{\bf {w}}} \newcommand{\pvel}{{\bf w}} \newcommand{\bW}{{\bf W}} \newcommand{\bw}{{\bf \hat{w}}} \newcommand{\bx}{{\bf \hat{x}}} \newcommand{\bxx}{{\bf x}} \newcommand{\bX}{{\bf X}} \newcommand{\bY}{{\bf Y}} \newcommand{\by}{{\bf \hat{y}}} \newcommand{\byy}{{\bf y}} \newcommand{\bz}{{\bf \hat{z}}} \newcommand{\bom}{\boldsymbol{\omega}} \newcommand{\bde}{\mathbf{\delta}} \newcommand{\bOm}{\boldsymbol{\Omega}} \newcommand{\bal}{\boldsymbol{\alpha}} \newcommand{\bomFE}{{\boldsymbol{\omega}}_{\cF/\cE}} \newcommand{\bomBA}{{\boldsymbol{\omega}}_{\cB/\cA}} \newcommand{\bGa}{\boldsymbol{\Gamma}} \newcommand{\btau}{\hat{\boldsymbol{\tau}}} \newcommand{\rot}{\boldsymbol{\tau}} \newcommand{\grad}{\boldsymbol{\nabla}} \newcommand{\iner}{{\cal I}_B} \newcommand{\inerG}{{\cal I}_G} \newcommand{\Earth}{\text{Earth}} \newcommand{\Arrow}{\mbox {$\longrightarrow$}} \newcommand{\half}{\frac{1}{2}} \newcommand{\al}{\alpha} \newcommand{\ep}{\epsilon} \newcommand{\ga}{\gamma} \newcommand{\te}{\theta} \newcommand{\la}{\lambda} \newcommand{\om}{\omega} \newcommand{\Om}{\Omega} \newcommand{\ro}{\rho} \newcommand{\Si}{\Sigma} \newcommand{\pSi}{{\partial \Sigma}} \newcommand{\bSi}{{\bar{\Sigma}}} \newcommand{\si}{\sigma} \newcommand{\dl}{\dot{l}} \newcommand{\ddl}{\ddot{l}} \newcommand{\dep}{\dot{\ep}} \newcommand{\ddep}{\ddot{\ep}} \newcommand{\ddbe}{\ddot{\beta}} \newcommand{\dbe}{\dot{\beta}} \newcommand{\dal}{\dot{\alpha}} \newcommand{\ddal}{\ddot{\alpha}} \newcommand{\ddga}{\ddot{\gamma}} \newcommand{\dphi}{\dot{\phi}} \newcommand{\ddphi}{\ddot{\phi}} \newcommand{\dpsi}{\dot{\psi}} \newcommand{\ddpsi}{\ddot{\psi}} \newcommand{\dte}{\dot{\te}} \newcommand{\ddte}{\ddot{\te}} \newcommand{\dom}{\dot{\om}} \newcommand{\dx}{\dot{x}} \newcommand{\ddx}{\ddot{x}} \newcommand{\dX}{\dot{X}} \newcommand{\ddX}{\ddot{X}} \newcommand{\dy}{\dot{y}} \newcommand{\ddy}{\ddot{y}} \newcommand{\dY}{\dot{Y}} \newcommand{\ddY}{\ddot{Y}} \newcommand{\dz}{\dot{z}} \newcommand{\dZ}{\dot{Z}} \newcommand{\ddz}{\ddot{z}} \newcommand{\ddZ}{\ddot{Z}} \newcommand{\Dp}{\dot{p}} \newcommand{\ddr}{\ddot{r}} \newcommand{\dr}{\dot{r}} \newcommand{\dq}{\dot{q}} \newcommand{\dQ}{\dot{Q}} \newcommand{\tq}{\tilde{q}} \newcommand{\ddq}{\ddot{q}} \newcommand{\dbq}{\dot{{\bf q}}} \newcommand{\ddbq}{\ddot{{\bf q}}} \newcommand{\dds}{\ddot{s}} \newcommand{\ds}{\dot{s}} \newcommand{\dro}{\dot{\ro}} \newcommand{\ddro}{\ddot{\ro}} \newcommand{\dv}{\dot{v}} \newcommand{\du}{\dot{u}} \newcommand{\bSi}{\overline{\Sigma}} \newcommand{\coB}{\overline{{\cal B}}} \newcommand{\kin}{\mathbb{K}} \newcommand{\qQ}{{\mathbb{Q}}} \newcommand{\pot}{{\mathbb{U}}} \newcommand{\hal}{{\mathbb{H}}} \newcommand{\lag}{{\mathbb{L}}} \newcommand{\gib}{{\mathbb{S}}} \newcommand{\energ}{{\mathbb{E}}} \newcommand{\danger}{\text{⚠}} \newcommand{\ddanger}{\text{⚠}} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \definecolor{fillinmathshade}{gray}{0.9} \newcommand{\fillinmath}[1]{\mathchoice{\colorbox{fillinmathshade}{$\displaystyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\textstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptscriptstyle\phantom{\,#1\,}$}}} \)

Section 15.2 Gyroscope: Definition

We start with a general definition of gyroscope.

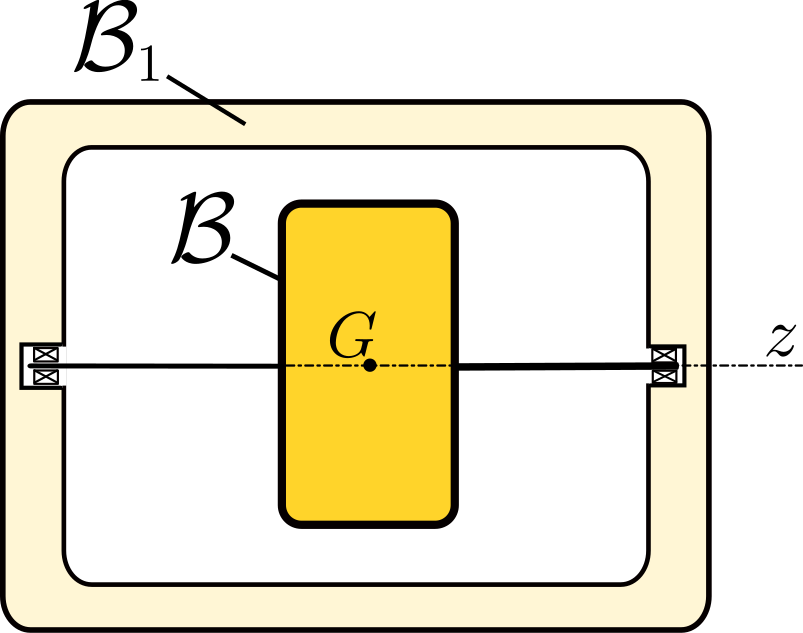
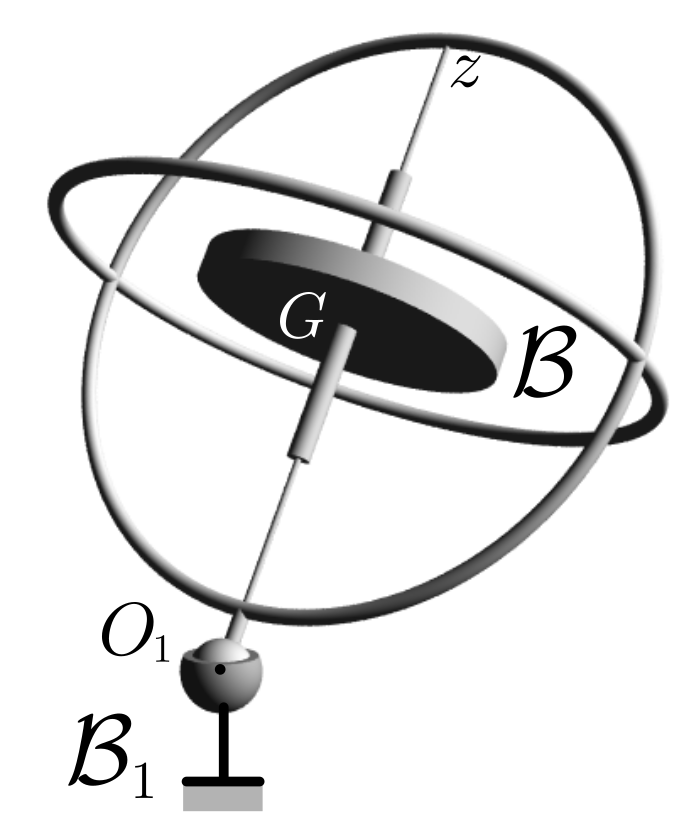
Definition 15.2.1. Gyroscope.

We call gyroscope a rigid body \(\cB\) in motion in a referential \(\cE\) with the following properties

Body \(\cB\) is an axisymmetric rigid body with respect to some axis \((G, \bz)\) passing through its mass center \(G\text{.}\) Its inertia operator about \(G\) is characterized by an axial moment of inertia \(C\text{,}\) and a transverse moment of inertia \(A\text{:}\)
\begin{equation} \cI_{G} ({\bf u}) = A ({\bf u} - ({\bf u}\cdot\bz) \bz ) + C ({\bf u} \cdot \bz) \bz\tag{15.2.1} \end{equation}
for any vector \({\bf u}\text{.}\)
The moment about axis \((G, \bz)\) of the external forces acting on \(\cB\) is zero:
\begin{equation} \bM_{G , {\coB} \to \cB} \cdot \bz = 0 .\tag{15.2.2} \end{equation}
Body \(\cB\) rotates with a large angular velocity \(\omega_z = \bom_{\cB / \cE} \cdot \bz\) about its axis.

Remark 15.2.2.

The axial angular velocity \(\om_z\) is large compared to the transverse component of \(\bom_{\cB / \cE}= \om_z \bz + \bOm_\perp\text{:}\) \(|\bOm_\perp| \ll |\omega_z|\text{.}\) However \(\om_z\) may not necessarily be large if the axial moment of inertia \(C\) is itself much larger than transverse moment of inertia \(A\text{.}\) In all cases, the magnitude of the axial angular momentum \(C |\omega_z|\) remains much larger than that of the transverse angular momentum \(A |\bOm_\perp|\text{.}\)

Remark 15.2.3.

A typical realization is shown in Figure 15.2.4 (left): an axisymmetric body \(\cB\) of axis \(Gz\) is connected by frictionless pivots to another body \(\cB_1\) which serves as a housing of the gyroscope. Body \(\cB_1\) is itself in motion relative to a referential \(\cE\) and its orientation relative to \(\cE\) is free to vary arbitrarily. If the external actions exerted on \(\cB\) amount to the forces of gravity and the contact reaction forces acting on the pivots, then these external forces satisfy \(\bM_{G , {\coB} \to \cB} \cdot \bz = 0\) irrespective of the motion of \(\cB_1\text{.}\)

Figure 15.2.4.

Another realization shown in Figure 15.2.5 amounts to constrain the axle \(Gz\) of \(\cB\) to body \(\cB_1\) by a frictionless spherical joint of center \(O_1\) located on the axis \(Gz\) of \(\cB\text{.}\) Then once again the condition \(\bM_{G , {\coB} \to \cB} \cdot \bz = 0\) is satisfied.

Figure 15.2.5.