Skip to main content

Advanced Engineering Dynamics

R. Valéry Roy

Section 11.5 Dynamic Balancing

Recall from Section Subsection 11.4.1 that the rotational motion of a rigid body about a fixed axis \((O, \bz_0)\) is governed by the equation
\begin{align*} - m e \dte^2 \amp = R_x + F_x \\ me \ddte \amp = R_y + F_y \\ 0 \amp = R_z + F_z \\ I_{Oxz} \ddte -I_{Oyz} \dte^2 \amp = M_x + N_x \\ I_{Oxz} \dte^2 + I_{Oyz} \ddte \amp = M_y + N_y \\ I_{Oz} \ddte \amp = N_z \end{align*}
These equations show that the inertial terms involving \(\dte^2\) can have a significant effect on the forces and moments exerted on the supporting bearings. For fast-rotating bodies, these inertial effects can lead to significant vibrations, noise, wear and possibly failure. It is important to minimize them. This can be achieved by a process known as dynamic balancing.
Figure 11.5.1.

Remark 11.5.3.

The condition of static balancing \(e=0\) states that mass center \(G\) must be located on the axis of rotation.

Remark 11.5.4.

The condition of dynamic balancing \(I_{Oxz} = I_{Oyz} =0\) states that the axis of rotation \((O, \bz_0)\) is a principal axis of inertia.
Hence, to guarantee the dynamic balancing of a rigid body one must alter its mass distribution, typically by adding or removing a pair of concentrated masses \((m_1,m_2)\) at locations \((P_1,P_2)\) fixed relative to body 1: the body is then replaced by the rigid system \(\Si \equiv \{ 1=, (P_1 , m_1) , (P_2 , m_2) \}\text{.}\) The masses \(m_1\) and \(m_2\) and the locations of \(P_1\) and \(P_2\) are determined by imposing conditions (11.5.1) for system \(\Si\text{.}\) Denote by \(\br_{OP_i } = x_i \bx_1 + y_i \by_1 + z_i \bz_0\text{.}\) Then, the mass center \(G_\Si\) and the products \(D_\Si\text{,}\) \(E_\Si\) are given by
\begin{equation*} (m+ m_1 + m_2) \br_{OG_\Si} = m \br_{OG} + m_1 \br_{OP_1} + m_2 \br_{OP_2} \end{equation*}
\begin{equation*} I_{Oyz,\Si} = I_{Oyz} - m_1 y_1 z_1 - m_2 y_2 z_2 \end{equation*}
\begin{equation*} I_{Oxz, \Si} = I_{Oxz} - m_1 x_1 z_1 - m_2 x_2 z_2 \end{equation*}
Then the conditions of dynamic balancing are satisfied by the equations
\begin{equation} \begin{array}{l} m e + m_1 x_1 + m_2 x_2 = 0 \\ m_1 y_1 + m_2 y_2 = 0 \\ I_{Oyz} - m_1 y_1 z_1 - m_2 y_2 z_2 = 0 \\ I_{Oxz} - m_1 x_1 z_1 - m_2 x_2 z_2 = 0 \end{array}\tag{11.5.2} \end{equation}
This gives four equations to solve for eight unknowns \((m_1 , m_2, x_1, y_1, z_1, x_2 , y_2 , z_2)\) infinitely many solutions are possible.

Remark 11.5.5.

Dynamic balancing cannot be achieved by the addition (or removal) of a single (point) mass.
In practice, constraints are placed on the locations \(P_1\) and \(P_2\) of the point masses, as is the case for the dynamic balancing of car tire/wheel assemblies. For instance, both points are placed at the same (prescribed) distance \(R\) from the axis of rotation and in two parallel planes \(z=0\) and \(z=h\text{.}\) They represents the locations for clip-on weights installed on the rim of car wheels. See Figure 11.5.6. Introducing the polar angles \(\phi_1\) and \(\phi_2\text{,}\) the coordinates of \(P_1\) and \(P_2\) are now
\begin{equation*} \br_{OP_1} = R(\cos\phi_1 \bx_1 + \sin\phi_1 \by_1), \qquad \br_{OP_2} = R(\cos\phi_2 \bx_1 + \sin\phi_2 \by_1)+ h \bz_0 \end{equation*}
Then, the four unknowns \((m_1, m_2, \phi_1, \phi_2)\) are found by solving the following four equations:
\begin{gather*} m e + m_1 R\cos\phi_1 + m_2 R\cos\phi_2 = 0 \\ m_1 \sin\phi_1 + m_2 \sin\phi_2 = 0 \\ I_{Oxz} - m_2 hR \cos\phi_2 = 0 \\ I_{Oyz} - m_2 hR\sin\phi_2 = 0 \end{gather*}
A unique solution is then found.
Figure 11.5.6. Two point masses \(P_1\) and \(P_2\) are placed on two parallel circles.

Example 11.5.7.

A flywheel of radius \(r\) is in rotation about a vertical axis \((O,\bz_0)\) at angular velocity \(\om (t) \bz_0\text{.}\) The axis \((O,\bv_1)\) of this body does not coincide with the vertical axis, due to a small error accounted by the small angle \(\epsilon\text{.}\) We neglect the thickness of the body (treated as a disk).
Figure 11.5.8.
  1. Find the moment of inertia \(I_{Ozz}\) and the products \(I_{Ozz}\) and \(I_{Oxz}\) as a function of angle \(\epsilon\) corresponding to axes \(Oxyz\text{.}\)
  2. Find a balancing solution for this system
Solution.
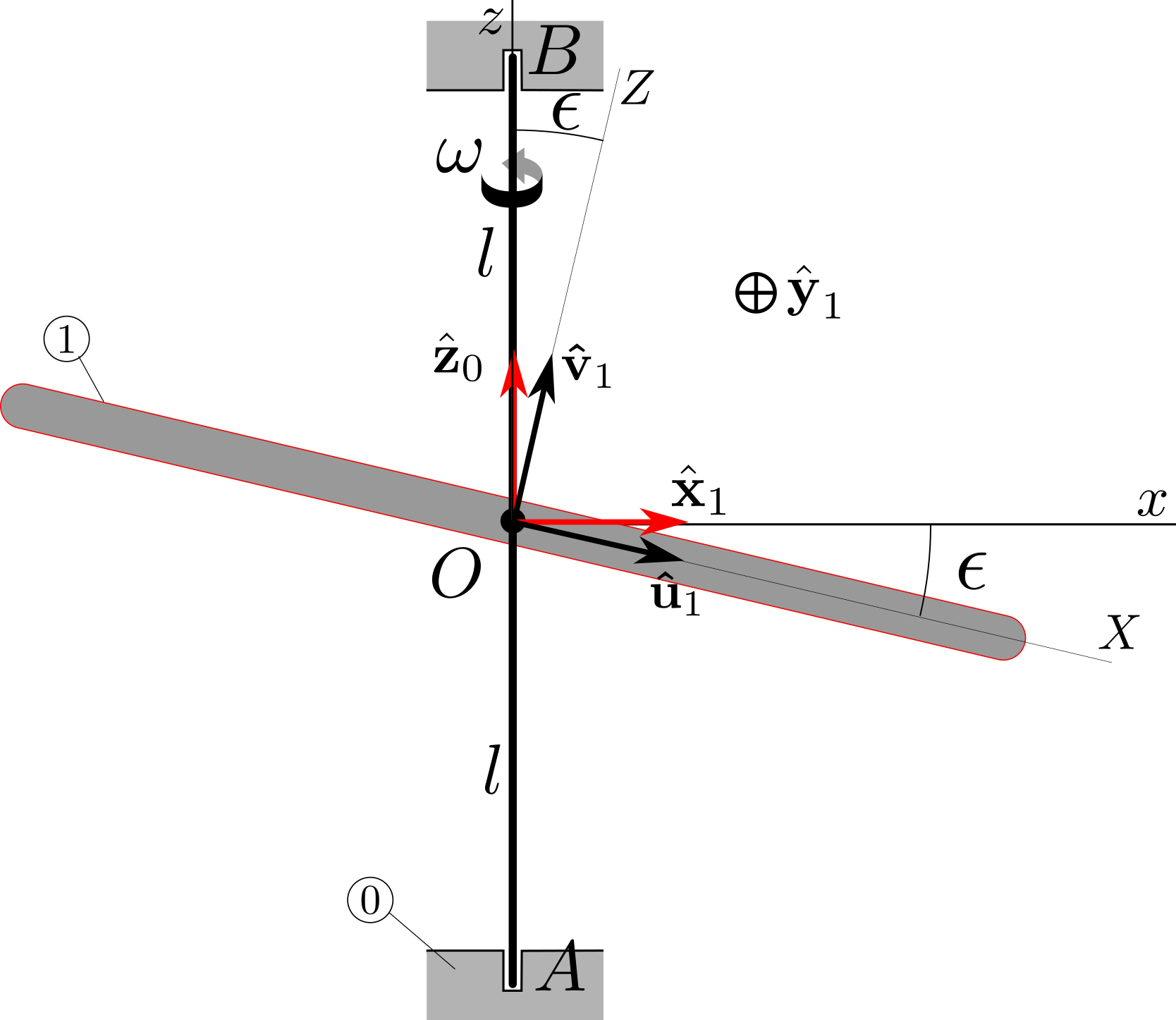
a. We expect \(I_{Oyz}=0\) by symmetry. We can find the moment/products \(I_{Ozz}\text{,}\) \(I_{Ozz}\) and \(I_{Oxz}\) from those about axes \(OXYZ\text{.}\) For instance
\begin{align*} I_{Ozz} \amp = \int (x^2 +y^2) dm = \int \Big( (X \cos\ep + Z \sin\ep)^2 + Y^2 \Big) dm\\ \amp = \int (X^2 \cos^2 \ep + Y^2) dm\\ \amp = \frac{1}{4}mr^2 (1+ \cos^2\ep) \end{align*}
where we used \(\int X^2 dm = \int Y^2 dm = \frac{1}{4}mr^2\text{.}\) Likewise we find
\begin{align*} I_{Oxz} \amp = - \int xz dm = -\int(X \cos\ep + Z \sin\ep)(-X \sin\ep + Z \cos\ep) dm\\ \amp = \int X^2 \cos\ep\sin\ep dm\\ \amp = \frac{1}{4}mr^2 \cos\ep \sin\ep \end{align*}
b. We use two points in plane \(Oxz\) of coordinates \(P_1 (l_1\cos\ep, 0,-l_1\cos\ep)\) and \(P_2 (-l_2\cos\ep, 0, l_2\cos\ep)\text{.}\) Static and dynamic balancing is imposed by the equations
\begin{gather*} m_1 l_1 \cos\ep = m_2 l_2 \cos\ep\\ m_1 l_1 \sin\ep = m_2 l_2 \sin\ep\\ \frac{1}{4}mr^2 \cos\ep \sin\ep = - (m_1 l_1^2 +m_2 l_2^2) \cos\ep \sin\ep \end{gather*}
A solution is supplied by imposing \(m_1 = m_2 =-\delta^2 m/8\) and \(l_1 = l_2 =r/\delta\) for \(1\lt \delta \lt 2\text{.}\) This solution is not practical, as substantial amounts of material need to be removed from the flywheel (\(m_1+m_2\) ranges from \(- m/4 \) to \(-m\text{!}\)).
PrevTopNext