Skip to main content

Advanced Engineering Dynamics

R. Valéry Roy

Section 15.5 The Gyroscopic Approximation

The conclusions drawn in Section 15.4} were specific to a gyroscope possessing a fixed point \(O\) under the destabilizing effect of gravity and with an axis initially at rest. Similar conclusions could be made under more general conditions. They can also be generalized for a gyroscope governed by equation (15.3.5): for a general perturbing moment \(\bM_G\) and for sufficiently small initial conditions, the change of orientation of its axis, quantified by the magnitude of \(d\bz/dt\text{,}\) remains very slow, of the order of \(1/C\om_z\text{,}\) as long as the axial angular speed \(\om_z\) is given a very large value. Furthermore, the axis is subject to high frequency nutational oscillations whose amplitude is of order \(1/\om_z^2\text{.}\)
In general, the analysis would be greatly simplified if the nutational effects were neglected. It is then tempting to neglect the inertial term \(A \bz \times \frac{ d^2 \bz}{dt^2}\) present in the equation of motion (15.3.5). However, it is easy to see that vector \(\tfrac{ d^2 \bz}{dt^2}\) is of the same order of magnitude as \(C \omega_z \tfrac{d\bz}{dt}\) (both are of order \(1\) in \(\om_z\text{.}\) and hence cannot be neglected at any given time. However vector \(\tfrac{ d^2 \bz}{dt^2}\) oscillates rapidly about a slowly-varying direction, and hence, on average becomes negligible. The gyroscope’s average motion can then be predicted by using the following approximation:

Remark 15.5.2.

To create a gyroscopic couple, the gyroscope’s axis must exhibit a rotation transverse to the axis. The resulting motion is often called gyroscopic drift.

Remark 15.5.3.

The gyroscopic drift is detrimental whenever the gyroscope must maintain a fixed direction, such as in inertial navigation systems.

Remark 15.5.4.

The gyroscopic drift effects can be exploited to detect external perturbations or to measure rotational motions.
The following example illustrates the use of the gyroscopic approximation. It demonstrates the unexpected behavior of gyroscopes.

Example 15.5.5.

Consider a gyroscope 3 mounted on two massless gimbals 1 and 2 in motion in a Newtonian referential 0. The outer gimbal 1 is connected to 0 by a frictionless pivot of vertical axis \((O, \bz_0)\) with corresponding angular velocity \(\bom_{1 /0} = \dpsi \bz_0\text{.}\) The inner gimbal 2 is connected to outer gimbal 1 by a frictionless pivot of horizontal axis \((O, \bu)\) with corresponding angular velocity \(\bom_{2/1} = \dte \bu\text{.}\) Finally gyroscope 3 of mass center \(O\) is mounted on 2 by a frictionless pivot of axis \((O, \bz)\) about which it rotates at angular velocity \(\bom_{3/2} = \dphi \bz\text{.}\)
Figure 15.5.6.
The gyroscopic assumptions are made: owing to the absence of axial moment \(\bM_{O, \bar{3} \to 3} \cdot \bz = 0\) and to the large axial angular velocity \(\dphi\text{,}\) the angular momentum of body 3 about \(O\) can be approximated as \(\bH_O = C \dphi \bz\text{,}\) where \(\dphi\) remains constant and where \(C\) is the axial moment of inertia of body 3. In the absence of external perturbations, the axis \((O,\bz)\) remains fixed relative to referential 0, its position given by constant angles \(\theta = \theta_0\) and \(\psi = \psi_0\text{.}\)
  1. The system is subjected to an external perturbation in the form of a force \(F_P \bz \times \bu = F_P \bw\) of constant magnitude \(F_P\) applied at point \(P\) of the gyroscope’s axis defined by \(\br_{OP}= - r\bz\) (\(r\) is a positive constant). Describe the dynamic response of the system to this perturbation.
  2. The system is now perturbed by applying a force \(F_Q \bz_0 \times \bu = F_Q \bv\) of constant magnitude \(F_Q\) applied at point \(Q\) of gimbal 1 defined by \(\br_{OQ}= R\bu\) (\(R\) is a positive constant). Describe the dynamic response of the system to this new perturbation.
Solution.
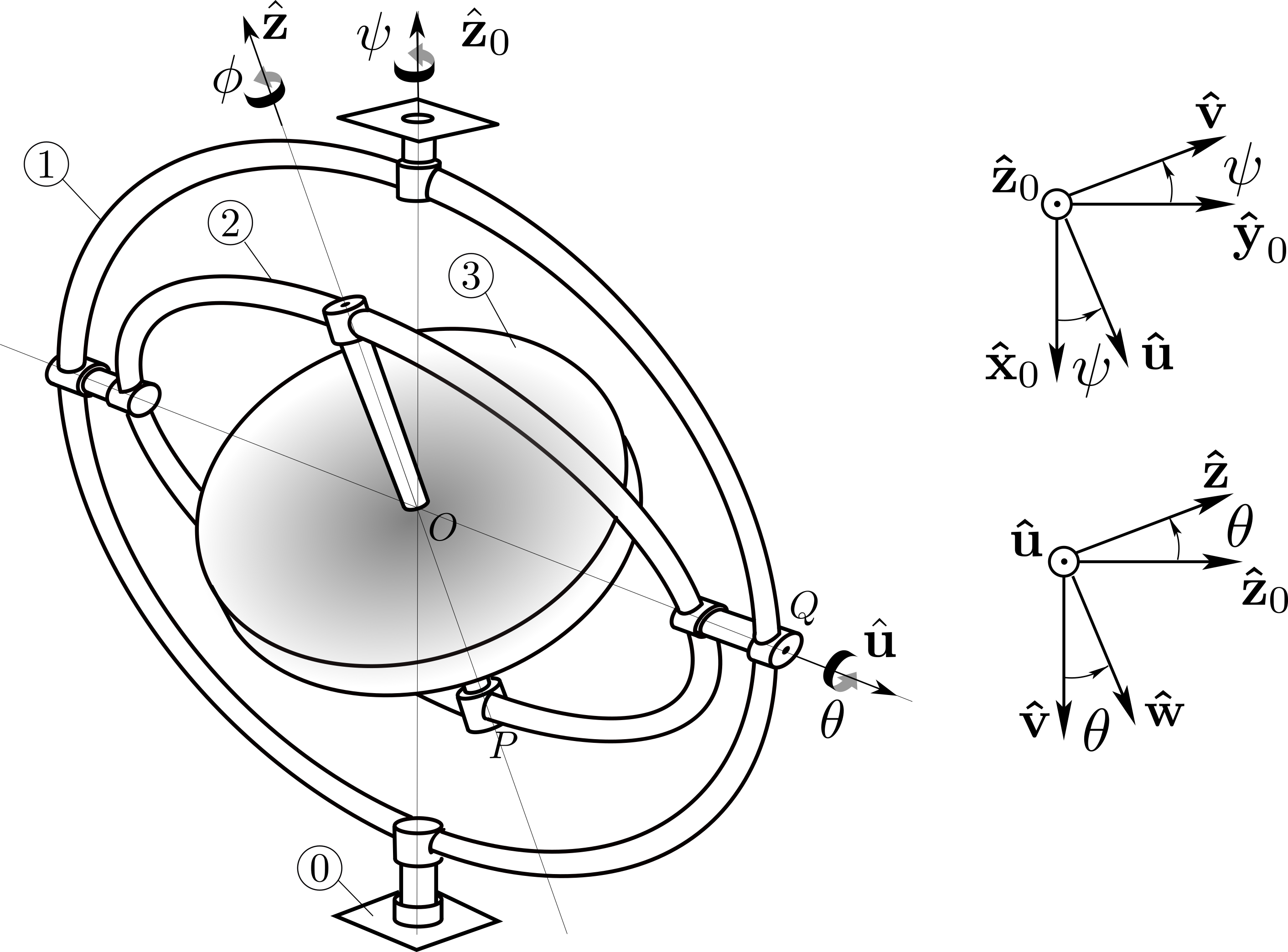
a. Force \(F_P \bw\) creates an external moment \(\bM_O = -r \bz\times F_P\bw = r F_P \bu\) applied to body 3. Application of the dynamic moment equation \(d\bH_O /dt = \bM_{O, \bar{3}\to 3}\) gives
\begin{equation*} C \dphi \frac{d\bz}{dt} = rF_P \bu + \bM^c_{O, 2 \to 3} \end{equation*}
To evaluate \(d \bz /dt\) we use the angular velocity \(\bom_{2 /0} = \dpsi\bz_0 + \dte \bu\text{:}\)
\begin{equation*} \frac{d\bz}{dt} = (\dpsi\bz_0 + \dte \bu) \times \bz = \dpsi \sin\te \bu - \dte \bw \end{equation*}
Hence we obtain
\begin{equation*} C \dphi (\dpsi \sin\te \bu - \dte \bw) = rF_P \bu + \bM^c_{O, 2 \to 3} \quad {(1)} \end{equation*}
Before resolving (1) on basis \((\bu, \bw, \bz)\) we need the components of \(\bM^c_{O, 2 \to 3} = L \bu + M \bw\) (the component on \(\bz\) is zero since the pivot between 2 and 3 is frictionless). They can be found by writing the ``equilibrium’’ of (massless) body 2:
\begin{equation*} \bM^c_{O, 3 \to 2} + \bM^c_{O, 1 \to 2} = \bze \end{equation*}
Since \(\bM^c_{O, 1 \to 2}\cdot \bu =0\text{,}\) this gives \(L=0\text{.}\) Then equilibrium of body 1 gives
\begin{equation*} \bM^c_{O, 0 \to 1} + \bM^c_{O, 2 \to 1} = \bze \end{equation*}
Again the condition \(\bM^c_{O, 0\to 1} \cdot \bz_0 = 0\) (the pivot between 0 and 1 is frictionless) necessarily implies \(M=0\text{.}\) Therefore, after taking into account \(L=M=0\text{,}\) equation (1) now leads to
\begin{equation*} \dte =0, \qquad C \dphi \dpsi \sin\te = rF_P \end{equation*}
This shows that angle \(\theta\) remains constant, and that the gyroscope slowly precesses at constant angular velocity
\begin{equation*} \dpsi = \frac{rF_P}{C \dphi \sin\te_0} \end{equation*}
about axis \((O,\bz_0)\text{.}\) One would expect that application of force \(F_P\) would lead to a rotation about axis \((O,\bu)\text{.}\) But in fact the gyroscope precesses at a right angle to the applied force.
b. Force \(F_Q \bv\) leads to a moment \(R \bu \times F_Q \bv = RF_Q \bz_0\) about \(O\) acting on body 1. Equilibrium of gimbal 1 translates into
\begin{equation*} RF_Q \bz_0 + \bM^c_{O, 0 \to 1}+ \bM^c_{O, 2 \to 1} = \bze \end{equation*}
Since \(\bz_0 \cdot \bM^c_{O, 0 \to 1} = 0\text{,}\) this leads to the equation
\begin{equation*} RF_Q + (M_{12}\bw + N_{12} \bz)\cdot\bz_0 = 0 \quad{(2)} \end{equation*}
where we have written \(\bM^c_{O, 2 \to 1} = M_{12}\bw + N_{12} \bz\) (the component on \(\bu\) is zero). On the other hand, equilibrium of body 2 implies that
\begin{equation*} \bM^c_{O, 3 \to 2} + \bM^c_{O, 1 \to 2} = \bze \quad {(3)} \end{equation*}
Since \(\bM_{O, 3 \to 2} \cdot \bz = 0\) this leads to \(N_{12} =0\text{.}\) Equation (2) then gives \(RF_Q = -M_{12} \sin\te\text{.}\) Finally we obtain from (3)
\begin{equation*} \bM^c_{O, 2 \to 3} = - \bM^c_{O, 2 \to 1} = - M_{12} \bw = \frac{RF_Q}{\sin\te} \bw \end{equation*}
Now as in a), we apply the dynamic moment equation \(d\bH_O /dt = \bM_{0, \bar{3}\to 3}\) to obtain
\begin{equation*} C \dphi (\dpsi \sin\te \bu - \dte \bw) = \bM^c_{O, 2 \to 3} = \frac{RF_Q}{\sin\te} \bw \end{equation*}
leading to
\begin{equation*} C \dphi \dpsi \sin\te = 0 , \qquad C \dphi \dte = -\frac{RF_Q}{\sin\te} \end{equation*}
This shows that angular velocity \(\dpsi\) is zero: the moment \(RF_Q \bz_0\) exerted on gimbal 1 does not lead to the rotation of gimbal 1 about axis \((O,\bz_0)\text{.}\) Instead it produces the rotation of gimbal 2 about axis \((O, \bu)\) with angular velocity
\begin{equation*} \dte = -\frac{RF_Q}{C \dphi \sin\te} \end{equation*}
This equation can be integrated to give
\begin{equation*} \cos\te = \cos\te_0 + \frac{RF_Q}{C \dphi} t \end{equation*}
which shows that angle \(\theta\) decreases toward the value \(\theta =0\text{:}\) gimbal 2 eventually reaches the vertical position, its plane coinciding with that of gimbal 1. At this point, the axes \((O,\bz_0)\) and \((O,\bz)\) coincide, the gyroscopic effect ceases, and the rotation of gimbal 1 proceeds.
PrevTopNext