Section 12.4 Potential Energy
We generalize in this section the notion of potential energy to the case of material systems subjected to mechanical actions. Consider two material systems \(\Sigma_1\) and \(\Sigma_2\) in motion relative to a referential \(\cE\text{.}\)
Subsection 12.4.1 Potential Energy Associated with External Actions
Definition 12.4.1. Potential Energy (External Action).
Material system \(\Sigma_2\) is said to possess a potential energy due to the action \(\{\cA_{\Si_1 \to \Si_2}\}\) relative to referential \(\cE\) if the corresponding power \(\Pow_{\Sigma _1 \rightarrow \Sigma _2 / \cE}\) can be written in the following form:
\begin{equation}
\Pow _{ \Sigma _1 \rightarrow \Sigma _2 / \cE} =
- \frac{d}{dt} \pot_{ \Sigma _1 \rightarrow \Sigma _2 / \cE}\tag{12.4.1}
\end{equation}
The action \(\left\{ \cA_{\Sigma _1 \rightarrow \Sigma _2} \right\}\) is then said to derive from potential energy \(\pot_{ \Sigma _1 \rightarrow \Sigma _2 / \cE}\) relative to referential \(\cE\) (within an arbitrary additive constant).
Note that an action \(\{\cA_{\Si_1 \to \Si_2}\}\) may derive from a potential \(\pot_{ \Sigma _1 \rightarrow \Sigma _2 / \cE}\) relative to a referential \(\cE\text{,}\) but not relative to another referential \(\cF\text{.}\)
Example 12.4.2.
Assuming that the Earth’s gravitational field can be modeled by a constant gravitational acceleration \(\bog\text{,}\) show that the corresponding potential energy \(\pot^g _{\text{Earth} \rightarrow \Sigma/ \cE}\) can be expressed as:
\begin{equation*}
\pot^g_{ \text{Earth} \rightarrow \Sigma / \cE} = - m_\Sigma \, {\bf g} \cdot {\bf r}_{OG_{\Sigma}}
\end{equation*}
relative to a referential \(\cE\) (of origin \(O\)) attached to Earth.
Solution.
If the local force \(\bF^g_{\text{Earth} \rightarrow \Sigma} (P)\) at every point \(P\) of \(\Si\) takes the expression \(\rho (P) \bog\) (where \(\rho\) is the mass density), then the power \(\Pow^g _{\text{Earth} \rightarrow \Sigma/ \cE}\) is given by
\begin{equation*}
\Pow^g _{\text{Earth} \rightarrow \Sigma/ \cE} = \int_\Si \rho (P) \bog \cdot \vel_{P/\cE} dV
= \int_\Si \frac{d}{dt} (\bog \cdot \br_{OP}) dm = \frac{d}{dt} (m_\Si \bog \cdot \br_{OG_\Si})
\end{equation*}
leading to the expression \(\pot^g_{ \text{Earth} \rightarrow \Sigma / \cE} = - m_\Sigma \, {\bf g} \cdot
{\bf r}_{OG_{\Sigma}}\text{.}\)
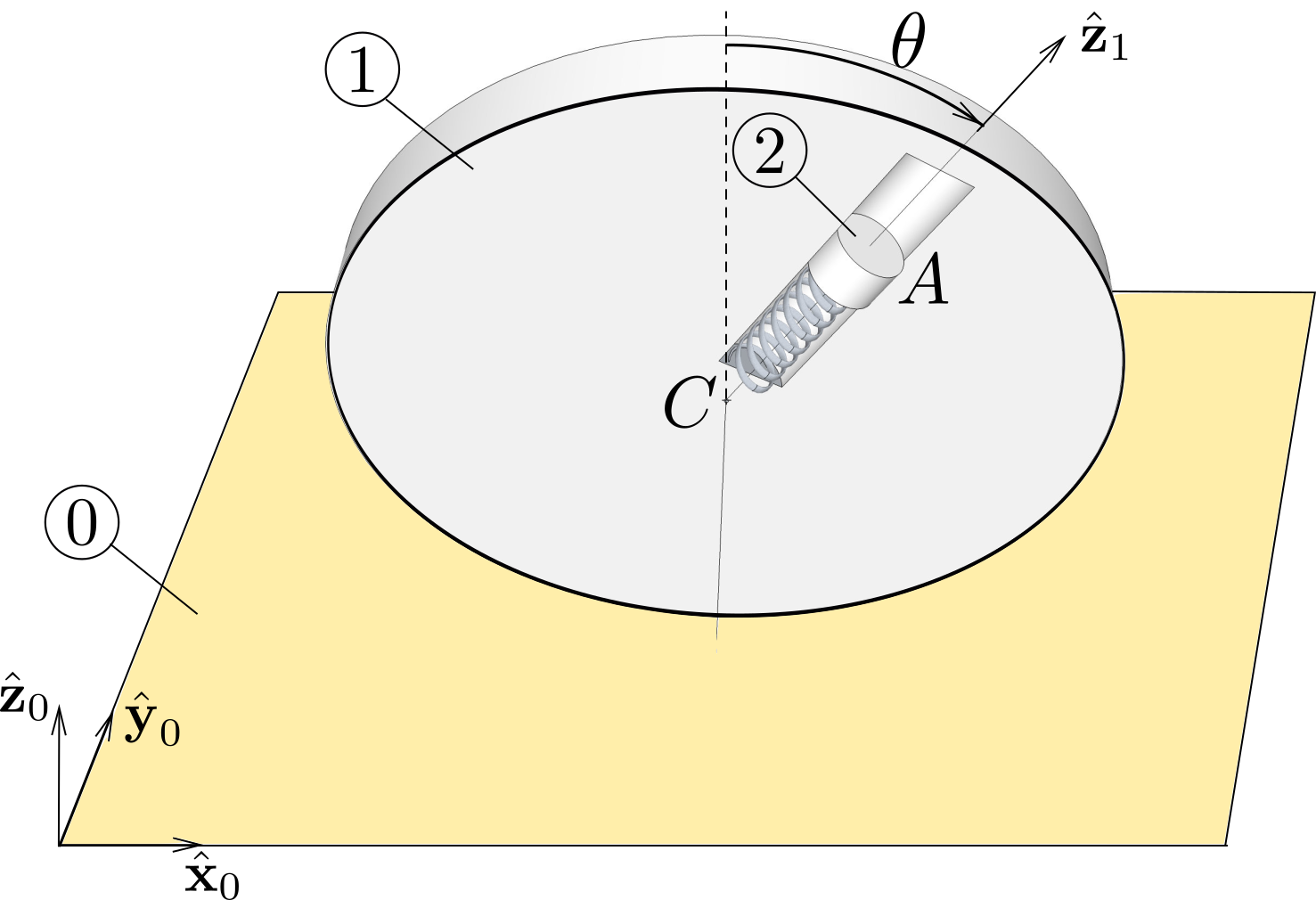
Example 12.4.3.
Figure 12.4.4 shows a wheel
1 of center
\(C\) and radius
\(R\) which rolls along the axis
\((O,\bx_0)\) of a referential
0\((O,\bx_0,\by_0,\bz_0)\text{.}\) A rigid body
2 is constrained to slide along a groove of
1 along the line
\((C,\bz_1)\text{.}\) The position of this system is defined by the variables
\(x(t) = \br_{OC}\cdot \bx_0\text{,}\) angle
\(\theta (t)
= (\bz_0 , \bz_1)\) and
\(l(t) = \br_{CA}\cdot \bz_1\) where
\(A\) is a point attached to
2. Body
2 is subjected to the following action
\begin{equation*}
\{\cA_{1\to 2}^{\text{s}}\}
=
\begin{Bmatrix}
-k (l-l_0) \bz_1 \\
\bze
\end{Bmatrix}
_A
\end{equation*}
due to the presence of a massless helicoidal spring mounted between
1 and
2 along line
\((C,\bz_1)\) (
\(k\) and
\(l_0\) are constants).
Show that action \(\{\cA_{1\to 2}^{\text{s}}\}\) derive from a potential \(\pot^{\text{s}}_{1 \rightarrow 2/ 1}\text{.}\)
Show that the power \(\Pow^{\text{s}}_{1 \rightarrow 2/ 0}\) cannot be determined from a potential \(\pot^{\text{s}}_{1 \rightarrow 2/ 0}\text{.}\)
Solution.
a. We can easily determine the power \(\Pow^{\text{s}}_{1 \rightarrow 2/ 1}\) as follows:
\begin{align*}
\Pow^{\text{s}}_{1 \rightarrow 2/ 1} \amp = \{\cA_{1\to 2}^{\text{s}}\} \cdot \{\cV_{2/1}\}\\
\amp =
\begin{Bmatrix}
-k (l-l_0) \bz_1 \\\\
\bze
\end{Bmatrix}
_A
\cdot
\begin{Bmatrix}
\bze
\\\\
\dot{l} \bz_1
\end{Bmatrix}
_A\\
\amp = -k (l-l_0) \dot{l} = -\frac{d}{dt}\Big( \frac{k}{2}(l-l_0)^2 \Big)
\end{align*}
which shows that potential \(\pot^{\text{s}}_{1 \rightarrow 2/ 1}\) exists and is given by
\begin{equation*}
\pot^{\text{s}}_{1 \rightarrow 2/ 1} = \frac{k}{2}(l-l_0)^2
\end{equation*}
b. We proceed as in the previous case to find power \(\Pow^{\text{s}}_{1 \rightarrow 2/ 0}\text{:}\)
\begin{align*}
\Pow^{\text{s}}_{1 \rightarrow 2/ 0} \amp = \{\cA_{1\to 2}^{\text{s}}\} \cdot \{\cV_{2/0}\}\\
\amp =
\begin{Bmatrix}
-k (l-l_0) \bz_1 \\
\bze
\end{Bmatrix}
_A
\cdot
\begin{Bmatrix}
\dte \by_0
\\
\dx \bx_0 + \dot{l} \bz_1 + l \frac{d\bz_1}{dt}
\end{Bmatrix}
_A\\
\amp = -k (l-l_0)(\dx \sin\theta+ \dot{l}) = -k(l-l_0) \dx\sin\te-\frac{d}{dt}\Big( \frac{k}{2}(l-l_0)^2 \Big)
\end{align*}
using the fact that \(\bz_1 \cdot d\bz_1/dt =0\text{.}\) We see that in this case we cannot define a potential \(\pot^{\text{s}}_{1 \rightarrow 2/ 0}\text{.}\)
Subsection 12.4.2 Potential Energy of Interaction
Definition 12.4.5. Potential Energy of Interaction.
Two interacting material systems \(\Si_1\) and \(\Si_2\) are said to possess a potential energy of interaction if the corresponding power of interaction \(\Pow _{ \Sigma _1 \leftrightarrow \Sigma _2}\) can be expressed in the form
\begin{equation}
\Pow _{ \Sigma _1 \leftrightarrow \Sigma _2} =
- \frac{d}{dt}\pot_{\Sigma _1 \leftrightarrow \Sigma_2} \tag{12.4.2}
\end{equation}
The interaction between \(\Si_1\) and \(\Si_2\) is then said to derive from potential energy \(\pot_{ \Sigma _1 \leftrightarrow \Sigma _2}\text{.}\)
Note that as power \(\Pow _{ \Sigma _1 \leftrightarrow \Sigma _2}\text{,}\) potential \(\pot_{ \Sigma _1 \leftrightarrow \Sigma _2}\) is independent of the referential \(\cE\) relative to which both material systems are observed.
Example 12.4.6.
Show that the potential energy associated with the gravitational interactions between \(\Sigma_1\) and \(\Sigma_2\) is given by:
\begin{equation*}
\pot^g_{\Sigma _1 \leftrightarrow \Sigma _2} = -
G \int_{\Sigma _1}\int_{\Sigma _2}
\frac{dm(P_1) dm(P_2)} {\left| {\bf r}_{P_1 P_2} \right|} .
\end{equation*}
Solution.
According to definition
(12.3.2) we can express
\(\Pow _{ \Sigma _1 \leftrightarrow \Sigma _2}\) as the sum
\(\Pow^g _{ \Sigma _1 \rightarrow \Sigma _2/ \cE}+\Pow^g _{ \Sigma _2 \rightarrow \Sigma _1/ \cE}\) relative to some arbitrary referential
\(\cE\text{:}\)
\begin{equation*}
\Pow^g _{ \Sigma _1 \leftrightarrow \Sigma _2} =
\int_{\Si_2} \bF^g_{1\to 2} (P_2) \cdot \vel_{P_2 / \cE} dV(P_2) +
\int_{\Si_1} \bF^g_{2\to 1} (P_1) \cdot \vel_{P_1 / \cE} dV(P_1)
\end{equation*}
with
\begin{equation*}
\bF^g_{1\to 2} (P_2) = - G \rho (P_2) \int_{\Si_1}\frac {\br_{P_1 P_2}}{|\br_{P_1 P_2}|^3} dm(P_1)
\end{equation*}
and
\begin{equation*}
\bF^g_{2\to 1} (P_1) = - G \rho (P_1) \int_{\Si_2}\frac {\br_{P_2 P_1}}{|\br_{P_1 P_2}|^3} dm(P_2)
\end{equation*}
leading to
\begin{align*}
\Pow^g _{ \Sigma _1 \leftrightarrow \Sigma _2} \amp = -G
\int_{\Si_1}\int_{\Si_2}
\frac {\br_{P_1 P_2}}{|\br_{P_1 P_2}|^3} \cdot (\vel_{P_2 / \cE} -\vel_{P_1 /\cE})
dm(P_1)dm(P_2)\\
\amp = -G
\int_{\Si_1}\int_{\Si_2}
\frac {\br_{P_1 P_2}}{|\br_{P_1 P_2}|^3} \cdot \frac{d\br_{P_1 P_2}}{dt}
dm(P_1)dm(P_2)
\end{align*}
As expected the integrand is independent of the choice of referential \(\cE\) and can be expressed as
\begin{equation*}
\frac {\br_{P_1 P_2}}{|\br_{P_1 P_2}|^3} \cdot \frac{d}{dt} \br_{P_1 P_2}
= - \frac{d}{dt} \left( {1\over |\br_{P_1 P_2}|} \right)
\end{equation*}
leading to the expression
\begin{equation*}
\Pow _{ \Sigma _1 \leftrightarrow \Sigma _2} = \frac{d}{dt} \int_{\Si_1}\int_{\Si_2}
G {dm(P_1)dm(P_2) \over |\br_{P_1 P_2}|}
\end{equation*}
This gives the result sought.