Section 12.3 Power of Internal Actions
We saw in
Section 12.1 that the sum of the powers generated by the internal forces acting between any two particles
\(P_i\) and
\(P_j\) of a system does not vanish, but is in fact independent of the choice of referential relative to which the motion of these particles is observed. This power was denoted
\(\Pow_{i\leftrightarrow j}\text{.}\) We seek a similar property for the case of material systems.
Consider two material systems \(\Sigma_1\) and \(\Sigma_2\) of a system \(\Sigma\) in motion relative to a referential \(\cE\text{.}\)
Definition 12.3.1. Power of Interaction.
The power of the interaction between two material systems \(\Si_1\) and \(\Si_2\) is defined as the sum of the powers generated by the action \(\left\{ \cA_{\Sigma _1 \rightarrow \Sigma _2} \right\}\) and by the reaction \(\left\{ \cA_{\Sigma_2 \rightarrow \Sigma_1} \right\}\) relative to \(\cE\text{:}\)
\begin{equation}
\Pow_{ \Sigma _1 \leftrightarrow \Sigma_2} =
\Pow_{ \Sigma _1 \rightarrow \Sigma_2 / \cE } +
\Pow _{ \Sigma _2 \rightarrow \Sigma_1 / \cE} \tag{12.3.1}
\end{equation}
Theorem 12.3.2.
The power of the interaction \(\Pow_{ \Sigma _1 \leftrightarrow \Sigma_2}\) between the material systems \(\Si_1\) and \(\Si_2\) is independent of the choice of referential \(\cE\text{.}\)
Proof.
Consider two referentials \(\cE\) and \(\cF\text{.}\) To compare the powers of the action and reaction in \(\cE\) and \(\cF\text{,}\) we determine the difference
\begin{equation*}
\underbrace{\Pow_{ \Sigma _1 \rightarrow \Sigma_2 / \cE } + \Pow_{\Sigma _2 \rightarrow \Sigma_1/\cE })}
_{\Sigma _1 \leftrightarrow \Sigma_2 / \cE }
-
\underbrace{(\Pow_{ \Sigma _1 \rightarrow \Sigma_2 / \cF }+ \Pow_{ \Sigma_2 \rightarrow \Sigma_1 / \cF} )}
_{\Sigma _1 \leftrightarrow \Sigma_2 / \cF }
\end{equation*}
We can simplify the power difference \((\Pow_{ \Sigma _1 \rightarrow \Sigma_2 / \cE }
-\Pow_{\Sigma _1 \rightarrow \Sigma_2/\cF })\) assuming that the action \(\{ \cA_{\Sigma _1 \rightarrow \Sigma _2}\}\) (and the reaction) is the result of contact forces \(\bof^c_{1 \rightarrow 2} (Q)\)
\begin{align*}
\Pow _{\Sigma _1 \rightarrow \Sigma _2 / \cE }
-
\Pow _{\Sigma _1 \rightarrow \Sigma _2 / \cF } \amp =
\int_{\partial\Sigma _2} \bof ^c_{1 \rightarrow 2} (Q) \cdot (\vel_{Q/\cE} - \vel_{Q/\cF}) dA\\
\amp =
\int_{\partial\Sigma _2} \bof ^c_{1 \rightarrow 2} (Q) \cdot \vel_{Q\in \cF/\cE} dA \\
\amp =
\{ \cA^c_{\Sigma _1 \rightarrow \Sigma _2} \} \cdot \{ {\cal V}_{ \cF / \cE } \}
\end{align*}
This last result also applies for gravitational interactions. Consequently, we have
\begin{equation*}
\Pow _{\Sigma _1 \leftrightarrow \Sigma_2 / \cE }-
\Pow _{\Sigma _1 \leftrightarrow \Sigma_2 / \cF } =
\left\{ \cA_{\Sigma _1 \rightarrow \Sigma _2} \right\} \cdot
\left\{ {\cal V}_{ \cF / \cE } \right\}
+
\underbrace{\left\{ \cA_{\Sigma _2 \rightarrow \Sigma _1} \right\} }_{
- \left\{ \cA_{\Sigma _1 \rightarrow \Sigma _2} \right\} } \cdot
\left\{ {\cal V}_{ \cF / \cE } \right\} = 0
\end{equation*}
This shows that the sum of the powers generated by the action \(\{ \cA_{\Sigma _1 \rightarrow \Sigma _2}\}\) and the reaction \(\{ \cA_{\Sigma _2 \rightarrow \Sigma _1}\}\) is independent of the chosen referential \(\cE\) relative to which the motions of \(\Sigma_1\) and \(\Sigma_2\) are observed.
Note that this property is implicit in the notation \(\Pow_{ \Sigma _1 \leftrightarrow \Sigma_2}\text{.}\) This last result can be used to determine the power of interaction between two rigid bodies \(\cB_1\) and \(\cB_2\) of a system \(\Si\text{.}\)
Theorem 12.3.3. Power of Interaction between Two Rigid Bodies.
The power of interaction between two rigid bodies \(\cB_1\) and \(\cB_2\) of a system \(\Si\) can be found as follows
\begin{align}
\Pow _{ \cB_1 \leftrightarrow \cB_2 } \amp = \Pow_{ \cB _1 \rightarrow \cB_2 / \cB_1} =
\{ \cA_{\cB_1 \rightarrow \cB_2} \} \cdot
\{ {\cal V}_{\cB_2 / \cB_1} \} \notag\\
\amp = \Pow _{ \cB _2 \rightarrow \cB_1/ \cB_2}
=
\left\{ \cA_{\cB _2 \rightarrow \cB _1} \right\} \cdot
\left\{ {\cal V}_{\cB_1 / \cB_2} \right\} \tag{12.3.2}
\end{align}
Example 12.3.6.
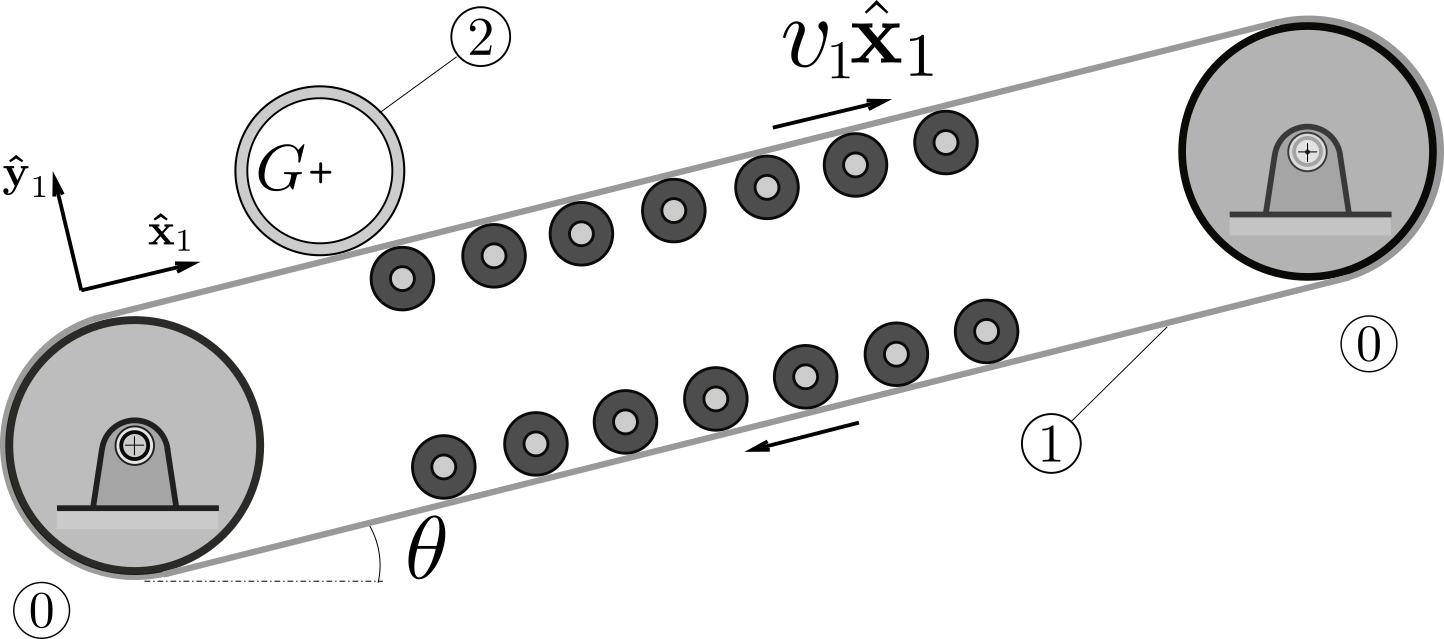
A cylindrical pipe 2 is pulled by a conveyor belt 1 in translational motion at velocity \(v_1 \bx_1\) relative to a referential 0. Neglect rolling frictional effects.
Find the expression of
the external power \(\Pow^c_{1\to 2/0}\) of the contact action exerted by body 1 on body 2,
the (internal) power \(\Pow^c_{1 \leftrightarrow 2}\) of interaction between body 1 and body 2.
Simplify these expressions when body 2 rolls without slipping on body 1.
Solution.
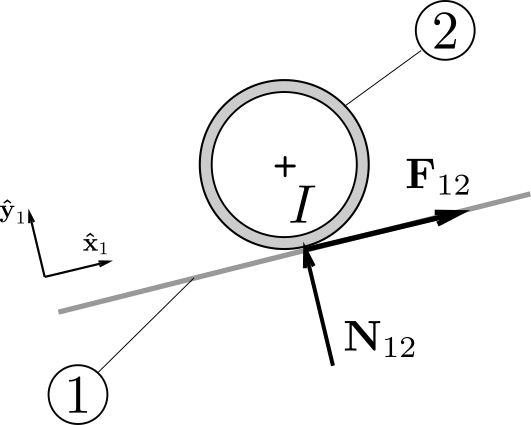
With the notations of
Figure 12.3.7 and
Figure 12.3.8, we write the contact action screw of body
1 on body
2 in the following form
\begin{equation*}
\{ \cA^c_{1 \rightarrow 2} \} =
\begin{Bmatrix}
N_{12} \by_1 + F_{12} \bx_1 \\
\bze
\end{Bmatrix}_I
\end{equation*}
From the point of view of body 2 in motion relative to referential 0, this action is external: its power (relative to referential 0) is found as
\begin{equation*}
\Pow^c_{1\to 2/0}= \{ \cA^c_{1 \rightarrow 2} \} \cdot \{ {\cal V}_{2 / 0} \}
=
\begin{Bmatrix}
N_{12} \by_1 + F_{12} \bx_1 \\
\bze
\end{Bmatrix}_I
\cdot
\begin{Bmatrix}
\bom_{2/0} \\
\vel_{I\in 2/0}
\end{Bmatrix}
\end{equation*}
This gives the expression
\begin{equation*}
\Pow^c_{1\to 2/0}=
(N_{12} \by_1 + F_{12} \bx_1 ) \cdot \vel_{I\in 2/0}
\end{equation*}
From the point of view of system \(\Si =\{1,2\}\text{,}\) this action is internal. The (internal) power of interaction is given by
\begin{equation*}
\Pow^c_{1 \leftrightarrow 2} = \Pow^c_{1 \to 2/1} =
\{ \cA^c_{1 \rightarrow 2} \} \cdot
\{ {\cal V}_{2 / 1} \}
=(N_{12} \by_1 + F_{12} \bx_1 ) \cdot \vel_{I\in 2/1}
\end{equation*}
This gives the expression
\begin{equation*}
\Pow^c_{1 \leftrightarrow 2 }= F_{12} \bx_1 \cdot \vel_{I\in 2/1}
\end{equation*}
since the slip velocity \(\vel_{I\in 2/1}\) is directed along \(\bx_1\text{.}\) Note that this power is always negative, since the friction force \(F_{12}\bx_1\) is always opposed to the slip velocity \(\vel_{I\in 2/1}\text{.}\) We do not know the sign of power \(\Pow^c_{1\to 2/0}\text{.}\)
When body 2 rolls without slipping, we have \(\vel_{I\in 2/1}= \bze\text{,}\) leading to
\begin{equation*}
\Pow^c_{1 \leftrightarrow 2} = 0
\end{equation*}
Using the kinematic identity \(\vel_{I\in 2/0}= \vel_{I\in 2/1}
+\vel_{I\in 1/0}= v_1 \bx_1\text{,}\) we find
\begin{equation*}
\Pow^c_{1\to 2/0}= (N_{12} \by_1 + F_{12} \bx_1 ) \cdot v_1 \bx_1 = v_1 F_{12}
\end{equation*}