Section 6.1 Transport Velocity and Acceleration
Consider the example of ant \(A\) walking toward the center \(O\) of a turntable \(\cF\text{,}\) itself in rotation about axis \(Oz\) of some referential \(\cE\text{.}\) See Figure 6.1.1(a). At any instant, there exists a point attached to \(\cF\) which coincides with the position \(A\) of the ant. We should not expect this point to have the same velocity as that of point \(A\) relative to referential \(\cE\text{,}\) since the motion of \(\cF\) is independent of that of \(A\text{.}\) Hence we must denote this velocity \(\vel_{A \in \cF / \cE}\) to ensure that this is the velocity of a point of frame \(\cF\) rather than that of point \(A\text{.}\) At instant \(t\text{,}\) a particular point of \(\cF\) coincides with the position of point \(A\text{.}\) At any other time, another point of \(\cF\) coincides with the position of \(A\text{.}\) Clearly, velocity \(\vel_{A \in \cF / \cE}\) cannot be obtained as \((d \br_{OA} /dt )_\cE =
\vel_{A/ \cE}\text{.}\) However the difference \(\vel_{A /\cE} - \vel_{A \in \cF / \cE}\) can be interpreted physically, as we will learn in Section 6.2.
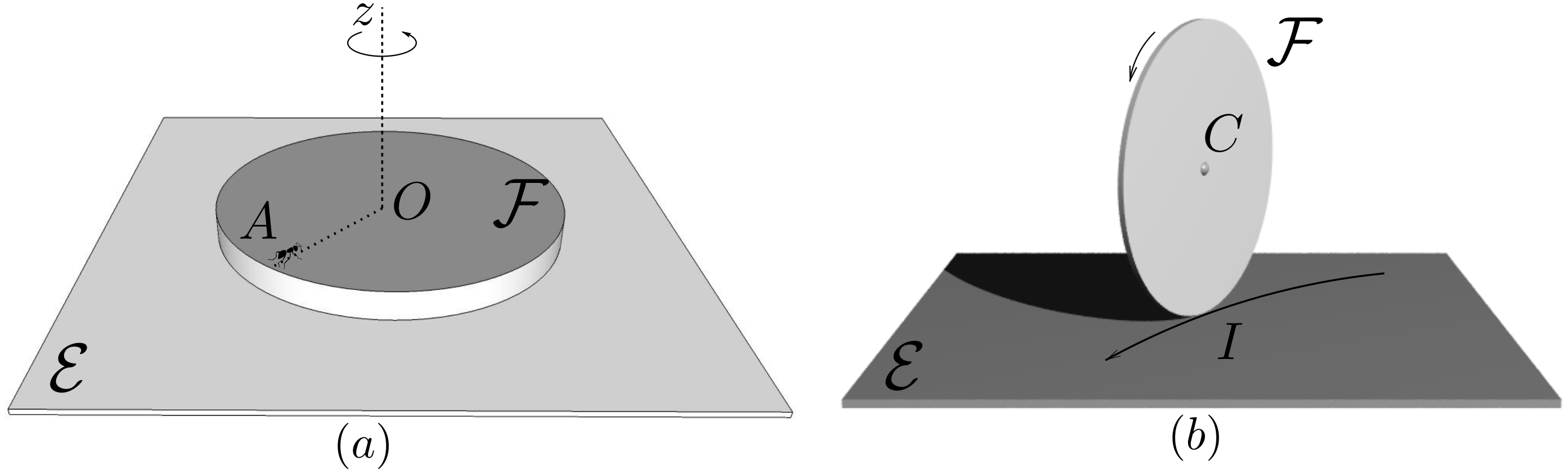
Consider as a second example the vertical disk \(\cF\) (of center \(C\)) which rolls on a horizontal support of a referential \(\cE\text{.}\) See Figure 6.1.1(b). Consider at a particular instant the point of contact \(I\) of the disk. At point \(I\text{,}\) there exist two possible ways of defining a velocity relative to \(\cE\text{:}\)
- the velocity of the point \(I\) moving along a curve of the horizontal plane, that is, along the locus described by the contact points as the disk rolls.
- the velocity of point \(I \in \cF\text{,}\) that is, of the point instantaneously attached to \(\cF\) and coinciding with the contact point.
Again, we should expect these velocities to be different, and we denote them as \(\vel_{I/\cE}\) and \(\vel_{I\in \cF / \cE}\text{,}\) respectively. In fact, if the disk rolls without slipping, we expect to have \(\vel_{I\in \cF / \cE} = \bze\) whereas \(\vel_{I/ \cE} = \vel_{C/\cE}
\neq \bze\text{.}\)

More generally, consider two referentials \(\cE\) and \(\cF\) in relative motion. Denote by \(O\) and \(B\) two points attached to \(\cE\) and \(\cF\text{,}\) respectively. See Figure 6.1.2. The motion of \(\cF\) relative to \(\cE\) is specified by the velocity \(\vel_{B/ \cE}\) and acceleration \(\ba_{B/\cE}\) of point \(B\text{,}\) and by its angular velocity \(\bom_{\cF/ \cE}\) and angular acceleration \(\bal_{\cF/ \cE}\text{.}\) Consider a point \(P\) in motion relative to both \(\cE\) and \(\cF\text{.}\) Its velocity relative to \(\cE\) is defined as
\begin{equation*}
\vel_{P/\cE}= \left( {d\br_{OP} \over dt} \right)_\cE
\end{equation*}
At any given time \(t\text{,}\) consider the point of \(\cF\) which coincides at this instant with the position of \(P\text{.}\) We denote its velocity relative to \(\cE\) as \(\vel_{P\in \cF / \cE}\) and call it transport velocity of \(P\) by referential \(\cF\) relative to \(\cE\text{.}\) This velocity is in general different from \(\vel_{P/\cE}\text{,}\) since it is the velocity of a point (instantaneously) attached to \(\cF\text{:}\) the only thing \(P\in \cF\) and point \(P\) have in common is their position in space at time \(t\text{.}\) The transport velocity of point \(P\) by \(\cF\) can be determined by relating it to another point of \(\cF\text{,}\) say \(B\text{,}\) according to the kinematic screw formula (3.6.1)
\begin{equation}
\vel_{P\in \cF / \cE} = \vel_{B / \cE} + \bom_{\cF / \cE} \times \br_{BP}\tag{6.1.1}
\end{equation}
As \(t\) varies, the points coinciding with \(P\) in \(\cF\) must occupy different physical positions within \(\cF\text{,}\) since point \(P\) is in motion relative to \(\cF\text{.}\)
In Section 6.2, we will learn how the three velocities, \(\vel_{P/ \cE}\text{,}\) \(\vel_{P /\cF}\) and \(\vel_{P \in \cF / \cE}\) relate to each other.
Likewise, we can define \(\ba_{P \in \cF / \cE}\) as the acceleration relative to \(\cE\) of the point of \(\cF\) coinciding with point \(P\) at time \(t\text{.}\) We call it transport acceleration of \(P\) by referential \(\cF\) relative to \(\cE\text{.}\) Again we should not expect that transport acceleration \(\ba_{P \in \cF /\cE}\) can be obtained by time-differentiation of velocity \(\vel_{P/\cE}\) or even of transport velocity \(\vel_{P\in \cF / \cE}\) whenever point \(P\) is in motion relative to \(\cF\text{:}\) point \(P\in \cF\) coincides with point \(P\) at time \(t\) only instantaneously.
We can, however, relate the transport acceleration \(\ba_{P \in \cF /\cE}\) to that of another point attached (at all times) to \(\cF\text{,}\) say point \(B\) of \(\cF\text{,}\) according to formula (5.5.1)
\begin{equation}
\ba_{P \in \cF /\cE} = \ba_{B / \cE} + \bal _{\cF/ \cE} \times
\br_{BP}
+\bom _{\cF/ \cE}\times(\bom _{\cF/ \cE}\times \br_{BP}) . \tag{6.1.2}
\end{equation}
As in the case of velocities, we will learn in Section 6.3 how the accelerations \(\ba_{P/ \cE}\text{,}\) \(\ba_{P /\cF}\) and \(\ba_{P \in \cF / \cE}\) are related to each other.
