Problems

Problems 5.6 Problems

1.

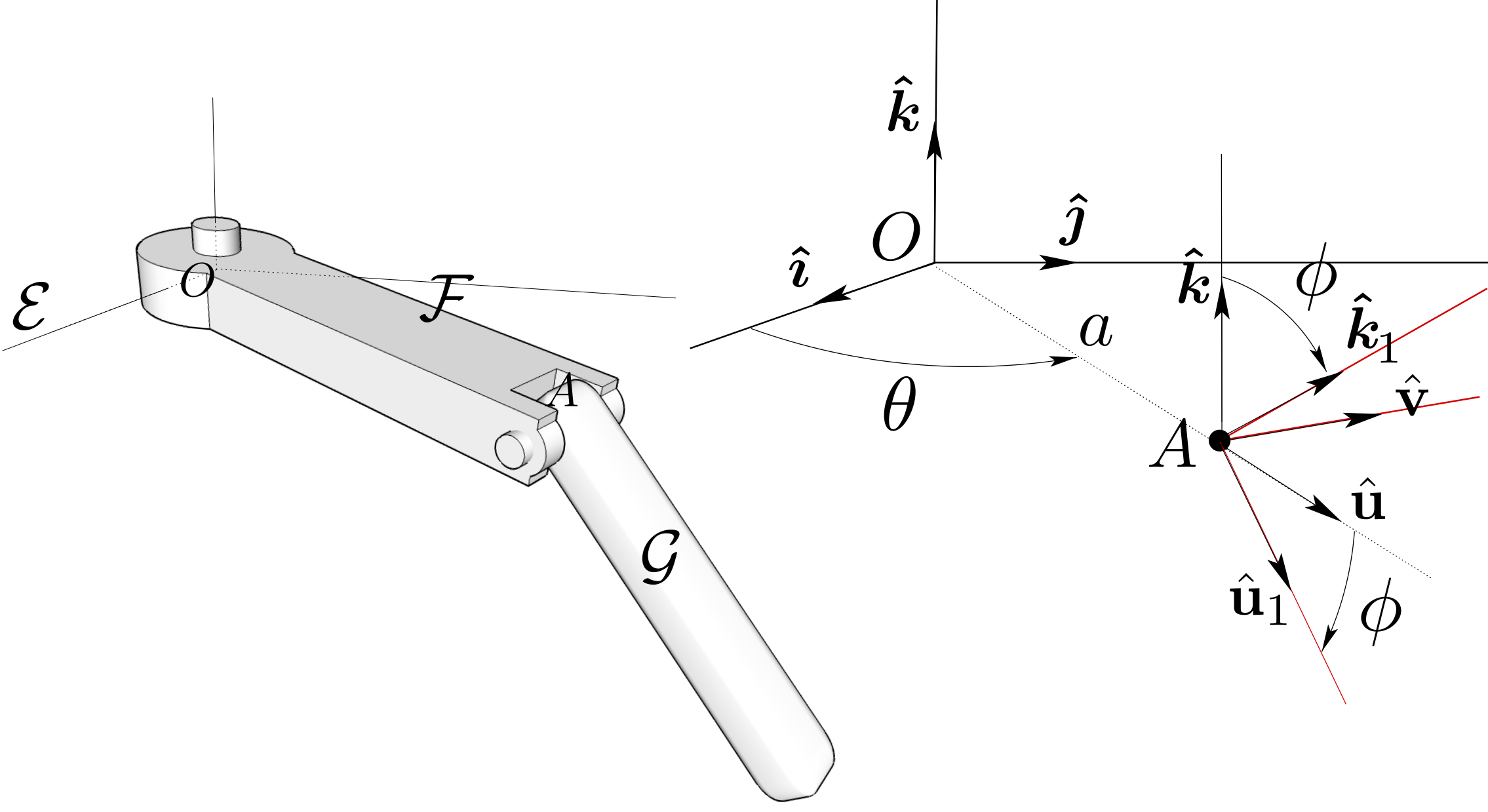
A rigid body \(\cB (B, \bhb_1, \bhb_2, \bhb_3)\) is in motion relative to referential \(\cA\text{.}\) At a particular time, its kinematic screw can be written in the following form

\begin{equation*} \left\{ \cV _{\cB/ \cA} \right\} = \left\{ \begin{array}{c} \bhb_1 + \om \bhb_2 \\ \bze \end{array} \right\}_P + \left\{ \begin{array}{c} \bhb_1 +\Om \bhb_2 \\ \bze \end{array} \right\}_Q \end{equation*}

where points \(P\) and \(Q\) are defined by \(\br_{BP} = \bhb_3\) and \(\br_{BQ} = -\bhb_3\) (\(\om\) and \(\Om\) are two real parameters).

Find the instantaneous screw axis of \(\cB\) relative to \(\cA\) at this instant. Can body \(\cB\) be in instantaneous rotation?

2.

A rigid body \(\cB\) is in motion relative to a referential \(\cE\text{.}\) Consider three points \(P_1\text{,}\) \(P_2\) and \(P_3\) attached to \(\cB\) and assumed to be non-collinear. Suppose that the velocities \(\vel_i \equiv \vel_{P_i /\cE}\text{,}\) \(i=1,2,3\text{,}\) are known at a given time.

Use Theorem 4.3.3 to derive an expression of the angular velocity \(\bom_{\cB / \cE}\) at this instant in terms of the velocities \(\vel_i\) and the position vectors \(\br_{ij} \equiv \br_{P_i P_j}\text{.}\)

3.

Consider three points \(A\text{,}\) \(B\text{,}\) and \(C\) in motion relative to a referential \(\cE (O, \be_1, \be_2, \be_3)\text{.}\) At a particular time their positions and velocities (relative to \(\cE\text{.}\) are known to be

\begin{equation*} \br_{OA} = \be_1 +\be_2 +\be_3, \qquad \vel_A = \be_1 + \be_3 \end{equation*}

\begin{equation*} \br_{OB} = - \be_1 + \be_3 , \qquad \vel_B = 2\be_1 -2 \be_2 + 3 \be_3 \end{equation*}

\begin{equation*} \br_{OC} = \be_1 - \be_2 , \qquad \vel_C = 2 \be_1 + \be_3 \end{equation*}

Show that these points belong to the same rigid body \(\cF\text{.}\)
Find the angular velocity \(\bom\) of \(\cF\) relative to \(\cE\text{.}\) Find the kinematic screw of \(\cF\text{.}\)
Find the instantaneous screw axis of \(\cF\) at this instant, and the corresponding pitch.

4.

It is possible to generalize the fundamental formula

\begin{equation*} \left( {d \buu \over dt } \right)_{\cA} = \left( {d \buu \over dt } \right)_{\cB} + \bom _{\cB/ \cA} \times \buu \end{equation*}

to a time-dependent screw \(\{\cU\}\text{.}\) Prove the following identity

\begin{equation*} \Big\{ \frac{d}{dt}\cU \Big\}_\cA =\Big\{ \frac{d}{dt}\cU \Big\}_\cB + \{ \cV_{\cB/\cA} \} \times \{\cU\} \end{equation*}

where the product \(\{ \cV_{\cB/\cA} \} \times \{\cU\}\) is defined in Exercise 4.10.9. In particular show that the identity

\begin{equation*} \Big\{ \frac{d}{dt}\cV_{\cB/\cA} \Big\}_\cA =\Big\{ \frac{d}{dt} \cV_{\cB/\cA} \Big\}_\cB \end{equation*}

is correct.

5.

In general, the acceleration field of points of a rigid body \(\cB\) in motion relative to a referential \(\cE\) does not define a screw, and hence is not equiprojective. We ask in this problem whether it is possible to find a subset of the body for which equiprojectivity of the accelerations holds.

Suppose that, at a given time, the accelerations of two points \(A\) and \(B\) of \(\cB\) are equiprojective. Then show that the angular velocity \(\bom_{\cB /\cE}\) is necessarily directed along line \(AB\) and that \(\vel_{A/\cE} = \vel_{B/\cE}\) at this instant.
Deduce the set of points of the body for which equiprojectivity of the accelerations holds.

6.

Consider rigid body \(\cA (A, \bha_1, \bha_2, \bha_3)\) in motion relative to a referential \(\cE\text{.}\) At a particular instant, the velocity (relative to \(\cE\)) of point \(A\) is \(\vel_A =v (2 \bha_1 + \bha_2 -3 \bha_3)\) (\(v\) is a positive scalar). Consider two other points \(B\) and \(C\) attached to \(\cA\) whose positions and velocities (relative to \(\cE\text{.}\) are given by, at this instant,

\begin{equation*} \br_{AB} = a (\bha_1 + \bha_2), \;\; \br_{AC}= a (\bha_1 + \bha_2+ \bha_3) \end{equation*}

\begin{equation*} \vel_B = v (3 \bha_2 - \bha_3), \;\; \vel_C = v (- \bha_1 + 2 \bha_2 -\bha_3) \end{equation*}

where \(a\) is a constant.

Determine the kinematic screw of \(\cA\) relative to \(\cE\) at this instant.
Find the corresponding instantaneous screw axis, and the equivalent representation of \(\{\cV_{\cA/\cE}\}\) in terms of the instantaneous screw axis.

Solution.

To find the kinematic screw of \(\cA\) relative to \(\cE\) (at that instant), we need to find \(\bom_{\cA/\cE} =\bom\text{.}\) We must solve equation
\begin{equation*} \bom \times \br_{BC}= \vel_C - \vel_B \end{equation*}
or (using basis \((\bha_1,\bha_2,\bha_3)\text{.}\)
\begin{equation*} \bom \times a \bha_3 = v(- \bha_1- \bha_2 ) \Longrightarrow \bha_3\times(\bom \times a \bha_3) = v\bha_3\times(- \bha_1- \bha_2 ) \end{equation*}
This gives only two components for \(\bom\text{:}\)
\begin{equation*} \bom = \om_3 \bha_3 + \frac{v}{a} (- \bha_2 + \bha_1) \end{equation*}
To find remaining component \(\om_3\) on \(\bha_3\text{,}\) we use equation \(\bom\times \br_{AB} = \vel_B -\vel_A\)
\begin{equation*} \bha_3 \times(\bom\times \br_{AB}) = \bha_3 \times(\vel_A -\vel_B) \end{equation*}
which gives (noting that \(\bha_3 \cdot \br_{AB} = 0\text{.}\)
\begin{equation*} - \om_3 \br_{AB} = v \bha_3 \times(- 2 \bha_1 + 2 \bha_2 +2 \bha_3) = 2 v (-\bha_2 - \bha_2)\Longrightarrow \om_3 = \frac{2v}{a} \end{equation*}
We conclude that \(\boxed{\bom= \frac{v}{a} (\bha_1 - \bha_2+ 2\bha_3)}\) and that
\begin{equation*} \{ \cV_{\cA / \cE} \} = \left\{ \begin{array}{cc} \displaystyle\frac{v}{a} (\bha_1 - \bha_2+ 2\bha_3) \\ \\ v (2 \bha_1 + \bha_2 -3 \bha_3) \end{array} \right\}_A \end{equation*}
To find instantaneous screw axis \(\Delta\text{,}\) we seek the points \(Q\) s.t. \(\vel_Q = p \bom\text{:}\)
\begin{equation*} \bom\times\br_{AQ} = p\bom - \vel_A \qquad{(1)} \end{equation*}
This equation necessarily implies that \(\bom \cdot (p\bom -\vel_A) = 0\text{:}\) this gives pitch \(p\)
\begin{equation*} \boxed{ p = \frac{\bom \cdot\vel_A}{\om^2} = -5a/6 } \end{equation*}
Then, we take the cross-product of (1) with \(\bom\text{:}\)
\begin{equation*} \bom\times(\bom\times\br_{AQ}) =\bom\times( p\bom - \vel_A) \Longrightarrow \la \bom - \bom^2\br_{AQ} = - \bom\times\vel_A \end{equation*}
where \(\la\) is unknown. Setting \(\la=0\) gives a particular point on \(\Delta\text{.}\) After evaluating the cross-product \(\bom\times\vel_A\text{,}\) we find that \(\Delta\) is defined as the set of points \(Q\) which satisfy
\begin{equation*} \br_{AQ} = \mu (\bha_1 - \bha_2+ 2\bha_3) +\frac{a}{6} ( \bha_1 +7 \bha_2 +3 \bha_3) \qquad (\mu \in \mathbb{R}) \end{equation*}
We can now write the kinematic screw as the sum
\begin{equation*} \{ \cV_{\cA / \cE} \} = \left\{ \begin{array}{cc} \bze \\ \\ \displaystyle -\frac{5v}{6} (\bha_1 - \bha_2+ 2\bha_3) \end{array} \right\} + \left\{ \begin{array}{cc} \displaystyle\frac{v}{a} (\bha_1 - \bha_2+ 2\bha_3) \\ \\ \bze \end{array} \right\}_{Q^*} \end{equation*}
where \(Q^*\) is the point defined by \(\br_{AQ^*} = \frac{a}{6} ( \bha_1 +7 \bha_2 +3 \bha_3)\text{.}\) This expresses the fact that body \(\cA\) is in helical motion about \(\Delta\) at the specified instant.

\(\blacksquare\)

7.

A point \(P\) moves in a referential \(\cE\) along a curve \(\cC\) at constant speed \(v_0\text{.}\) The tangential unit vector \(\be_t\text{,}\) normal unit vector \(\be_n\) and binormal unit vector \(\be_b = \be_t \times \be_n\) of curve \(\cC\) form a right-handed basis (the so-called Serret-Frenet basis). Consider the referential \(\cF (P, \be_t , \be_n , \be_b)\) defined by particle \(P\) and by the Serret-Frenet basis following the motion of \(P\) along \(\cC\text{.}\)

Find the angular velocity \(\bom_{\cF / \cE}\text{.}\)
Find the instantaneous screw axis \(\Delta\) of the motion of \(\cF\) relative to \(\cE\) in terms of the radius of curvature \(\rho\) and the radius of torsion \(\tau\) of curve \(\cC\) at \(P\text{.}\)
Find the instantaneous velocity taken on \(\Delta\text{.}\)
Under what condition is the motion of \(\cF\) relative to \(\cE\) an instantaneous rotation at any given time?

Hint.

Use the Serret-Frenet formulas found in Section 2.4.

Solution.

Recall that for any vector \(\bA\) fixed in referential \(\cF\) we have
\begin{equation*} \left({ d \bA \over dt } \right)_{\cE} = \bom_{\cF /\cE} \times \bA \end{equation*}
Let \(\bom_{\cF /\cE} = \bom = p \be_t + q \be_n + r \be_b\text{.}\) Then we have the following equations
\begin{equation*} \left({ d \be_t \over dt } \right)_{\cE} = (p \be_t + q \be_n + r \be_b) \times \be_t = r \be_n - q \be_b \qquad{(1)} \end{equation*}

\begin{equation*} \left({ d \be_n \over dt } \right)_{\cE} = (p \be_t + q \be_n + r \be_b) \times \be_n = p \be_b - r \be_t \qquad{(2)} \end{equation*}

\begin{equation*} \left({ d \be_b \over dt } \right)_{\cE} = (p \be_t + q \be_n + r \be_b) \times \be_b = q \be_t - p \be_n \qquad{(3)} \end{equation*}
Recall Serret-Frenet formulas
\begin{equation*} {d \be_t \over ds} = {1 \over \rho}\, \be_n , \qquad {d \be_n \over ds} = - {1 \over \rho}\, \be_t + {1\over\tau}\, \be_b, \qquad {d \be_b \over ds} = - {1 \over \tau} \, \be_n \qquad{(4)} \end{equation*}
where \(s(t)\) is the arclength measured on the (oriented) trajectory of particle \(P\text{.}\) Comparing equations (1-3) with (4) gives the angular velocity of referential \(\cF\text{:}\)
\begin{equation*} \boxed{ \bom = v_0 ( {\be_t \over \tau} + {\be_b \over \ro} ) } \end{equation*}
where we have used the expression \(ds/dt = v_0\) for the speed of \(P\text{.}\)

The instantaneous screw axis \(\Delta\) of \(\cF\) is the line \((I, \bom)\text{,}\) where point \(I\) has the instantaneous position
\begin{equation*} \br_{PI}= {\bom \times \vel_{P/\cE} \over \bom^2} = {\ro \over 1 + {\ro^2 \over \tau^2}} \be_n \end{equation*}

The points of \(\Delta\) have the velocity

\begin{equation*} \frac{\bom\cdot\vel_P}{\bom^2 } \bom = \frac{v_0}{1 + \frac{\tau^2}{\ro^2}} (\be_t + \frac{\tau}{\ro} \be_b) \end{equation*}

The pitch \(p= (1/\tau)/(1/\tau^2+ 1/\ro^2)\) vanishes in the limit \(1/\tau\to 0\text{.}\) Hence, the motion of \(\cF\) relative to \(\cE\) is an instantaneous rotation when curve \(\cC\) is planar.

\(\blacksquare\)

8.

Two rigid bodies \(\cF (O , \bu , \bv , \bk)\) and \(\cG (A, \bu_1 , \bv , \bk_1)\) are in motion in a referential \(\cE (O, \bi , \bj , \bk)\text{.}\) The motion of \(\cF\) relative to \(\cE\) is a rotation about axis \((O, \bk)\) of \(\cE\) with angular velocity \(\bom _{\cF / \cE} = \om_1 \bk\text{.}\) At time \(t=0\text{,}\) the bases \((\bi , \bj , \bk)\) and \((\bu , \bv , \bk)\) coincide. The motion of \(\cG\) relative to \(\cF\) is a rotation about axis \((A, \bv)\) of \(\cF\) with angular velocity \(\bom _{\cG / \cF} = \om_2 \bv\text{.}\) Point \(A\) is defined by \(\br_{OA} = a \bu\) (\(a\) is a constant).

Find the kinematic screw of \(\cG\) relative to \(\cE\) and the corresponding instantaneous screw axis.
Find and sketch the trajectory viewed from \(\cE\) of the point \(B\) attached to \(\cG\) whose initial position is given by \(\br_{OB} = 2a \bu\text{.}\)

9.

Consider three rigid bodies \(\cB_1\text{,}\) \(\cB_2\) and \(\cB_3\) in relative motion. Denote by \(\Delta_{ij} = \Delta_{ji}\) the instantaneous screw axis which characterizes the relative motion between bodies \(\cB_i\) and \(\cB_j\text{.}\)

Show that the three axes \(\Delta_{12}\text{,}\) \(\Delta_{23}\text{,}\) \(\Delta_{31}\) admit a common perpendicular line.
Assuming that rigid bodies \(\cB_1\text{,}\) \(\cB_2\) and \(\cB_3\) are in relative planar motion as shown in Figure 5.6.2, characterize the property shown in question a.

Prev Top Next