In this tutorial, we consider the simulation of a simple pendulum shown in the Figure. The application of the laws of motion gives the following ODE governing angle $\theta (t)$: $$ \ddot{\theta} + \omega_0^2 \sin\theta = 0 \qquad \text{(1)} $$ with $\omega_0^2 = g/l$ (in the absence of frictional effects). Given initial conditions $(\theta_0, \dot{\theta}_0)$ at time $t=0$, the solution of the ODE gives the functions $(\theta(t), \dot{\theta}(t))$ versus time $t$. We want to find a numerical solution of (1).
To accomplish this, we can use the ODE integrator of
the SciPy library. Located in the integrate module, the function odeint is
loaded as follows
from scipy.integrate import odeint
As for all ODE numerical integrators, the 2nd-order ODE must be converted to a system
of 2 first-order ODEs governing $(\theta,\dot{\theta})$:
$$
\frac{d\theta}{dt}= \dot{\theta}, \qquad
\frac{d\dot{\theta}}{dt}= - \omega^2 \sin{\theta} \qquad \text{(2-3)}
$$
So we define a function in python which returns the right-hand-side of system (2-3):
def pendulum(y, t):
theta, dtheta = y
return [dtheta, -omega0**2 *np.sin(theta)]
We then define an array of time values and initial conditions
omega0 = 0.1 # in [rad/s]. This is a frequency: omega0= sqrt(g/l)
theta0= 3*np.pi/4
dtheta0=0
T0=2.0*np.pi/omega0 # in [s]: this gives the period of oscillations in the linear regime
print('T0 = ',T0,'s')
tmax= 5*T0
t = np.linspace(0, tmax, 500)
We can now call function odeint of scipy: this integrates the two ODEs (3-4) by taking as input:
pendulum which defines the r.h.s. of (2-3)(theta0,dtheta0)ttheta, dtheta = odeint(pendulum, (theta0, dtheta0), t).T
Note that odeint returns an array of 2 columns. So we first need to apply the transpose (.T)
to the array to obtain 2 rows, which can then be assigned to arrays theta and omega.
We can verify that the total mechanical energy $E= \frac{1}{2}\dot{\theta}^2 + \omega_0^2 (1-\cos\theta)$ is conserved by computing and plotting the kinetic, potential and total energies during the motion.
Kin = 1./ 2.0 *dtheta** 2
Pot = omega0**2*(np.cos(theta0)-np.cos(theta) )
Emech = Kin + Pot # total mechanical energy
The rest of the script defines the graphical output. The python script can be found here. You could modify it by adding graphical plots of $\theta$ and $\dot{\theta}$ vs $t$. Here is the energy plot:
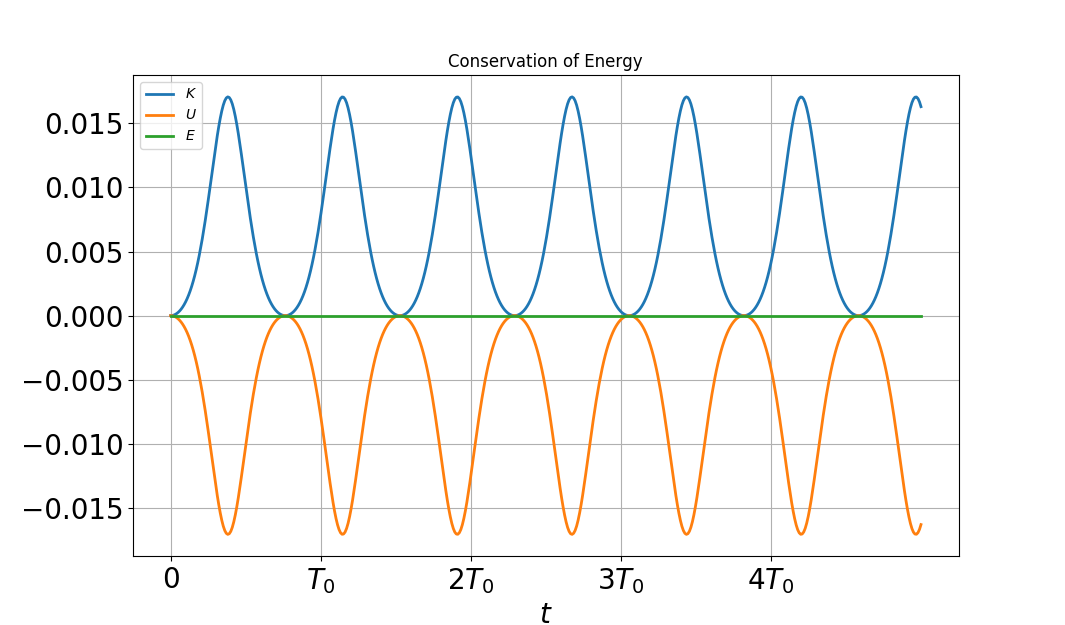A crude integration of the ODE would not guarantee conservation of energy.
Another version would involve the computation of the phase diagram, that is, the plot of trajectories in
the plane $(\theta, \dot{\theta})$ corresponding to different initial conditions $(\theta_0, 0)$.
The python script can be found
here. The phase portrait is incomplete, since it contains only periodic trajectories. Other trajectories are missing (which ones?). Find a way to complete it by adding a few of these missing trajectories.
In general, if you want to integrate a dynamic system modeled by a system of ODEs, you will have to put the system in the form of $N$ first-order ODEs, assuming $N$ independent variables $(y_1, y_2, \ldots, y_N)$:
$$
\frac{dy_1}{dt} = F_1 (y_1, y_2, \ldots, y_N)
$$
$$
\frac{dy_2}{dt} = F_2 (y_1, y_2, \ldots, y_N)
$$
$$
…
$$
$$
\frac{dy_N}{dt} = F_N (y_1, y_2, \ldots, y_N)
$$
You would then have to define a python function
def myODEsystem(y, t):
[y1,y2,..,yN] = y
return [F1, F2, ..., FN]
As an example in dimension $N=3$ consider the Lorenz system which displays chaotic dynamics: $$ \frac{dx}{dt}= \sigma (y-x) $$ $$ \frac{dy}{dt}= \rho x -y - xz $$ $$ \frac{dz}{dt}= -\beta z +xy $$ with the parameters $\sigma=10$, $\beta= 8/3$, $\rho = 28$ and initial conditions.
We would define the following python function
def Lorenz(X,t,sigma,beta,rho)
"""The Lorenz equations"""
x,y,z = X
F1= sigma*(y-x)
F2= rho*x-y-x*z
F3= -beta*z+x*y
return F1,F2,F3
The script is here.