
The course aims to provide Mechanical Engineering students in their sophomore year with the fundamentals of Dynamics. The emphasis is on understanding the physical principles governing motion of rigid bodies and applying them to solve engineering problems. This course has a strong component on modeling and simulation.
Prerequisite: Grade of C- or better in MEEG112 or equivalent.
R. Valéry Roy, A First Course in Engineering Dynamics, (2nd Edition), Hyperbolic Press, 2016.
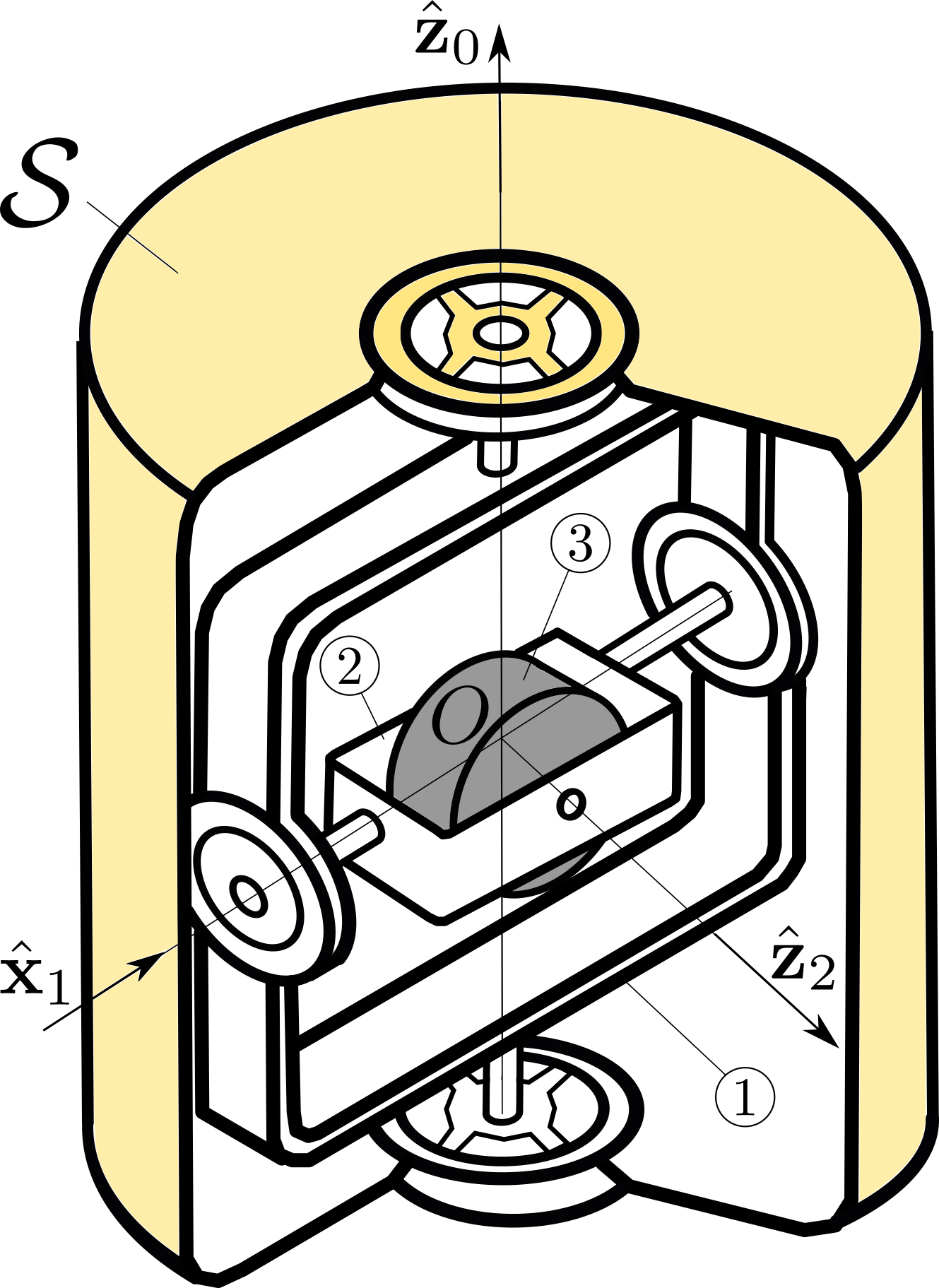
This course treats the study of the motions of material systems and the mechanical actions responsible for these motions. Material systems are assumed to be rigid bodies. The course starts with the topic of Kinematics, that is, the study of the motion of particles and rigid bodies without reference to the physical causes (forces) of the motion. Kinematics is the foundation of this course. The ultimate goal is the formulation of equations of motion and the extraction of information from these equations. This may include the search for first integrals of motion, the study of stability of a particular motion, the determination of external forces/moments to guarantee a particular trajectory, etc.
R. Valéry Roy, Advanced Engineering Dynamics, Second Edition, Hyperbolic Press, (2018).

This course exposes graduate students to fundamental mathematical concepts with applications to enginnering problem. Specifically, four topics are covered: (i) Complex Analysis, (ii) Green’s function, (iii) Variational Calculus and (iv) Asymptotic Analysis. Emphasis is placed on problem-solving and application to mechanical engineering problems.
I. Complex Analysis: 1. Complex numbers, complex variables. 2. Analytic functions. 3. Multivalued functions, branch points, branch cuts. 4. Integration in the complex plane. 5. Cauchy’s theorem. 6. Derivatives of analytic functions, Taylor and Laurent series, singularities. 7. Conformal Mapping.
II. Green’s Functions: 1. Generalized functions and Dirac’s delta function. 2. Green’s Functions for one-dimensional boundary value problems. 3. Green’s function for the Poisson equation. 4. Green’s function for the Helmholtz operator and the diffusion operator.
III. Calculus of Variations: 1. Examples of variational problems. 2. The Euler-Lagrange equation. 3. Constraints and Lagrange multipliers. 4. The Second Variation. 5. Multi-dimensional Variational Problems. 6. Examples in mechanics: Hamilton’s Principle, Optimal control.
IV. Asymptotic Analysis: 1. Dimensional analysis and basic definitions. 2. Asymptotic solution of algebraic equations. 3. Asymptotic expansion of integrals. 4. Regular Perturbation of ODEs and PDEs. 5. Singular Perturbation of ODEs: Asymptotic matching, Boundary layer theory, WKB approximation. 6. Multiple scales analysis of temporal systems. 7. The method of homogenization: application to the diffusion equation.

Many natural and technological processes involve phenomena which take place over widely differing scales of time and space. The advent of novel micro and nanofabrication techniques is challenging the scientific community to design engineering structures with submicrometer feature size in many fields of applications. New technologies offer the designer the ability to tailor complex 3D architectures, with unprecedented effective properties which are unmatched by their single-phase homogeneous counterparts. The development of these new technologies also hinges on comprehensive theoretical modeling and computational predictions.
Multiscale systems pose considerable difficulties. Traditional monoscale approaches are inadequate, even with sustained progress in computational power, hence the need for systematic multiscale modeling and simulation methods.
The role of multiscale methods is to provide the link between the microscopic features of a material and its macroscopic properties. They provide a fundamental understanding of how microstructure affects a material’s properties and performance. Although the microscopic details of the system have a significant effect on its behavior, we are often not interested in the knowledge of its behavior on the smallest scale. In fact, such solutions are not computationally feasible.
This course is organized in three parts:
Part 1: a presentation of exact or approximate mathematical methods for the modeling of multiscale materials,
Part 2: an introduction to computer simulation/numerical techniques for the study of multiscale materials,
Part 3: a study of some engineering applications where multiscale materials play a fundamental role.
Introduction
Examples of multiscale materials.
The challenge of multiscale problems & goals of a multiscale theory.
Historical Background.
Part I: Theory
Effective Medium Theory: Maxwell–Garnett Theory, Bruggeman Theory, Green’s functions formulation.
Bergman’s spectral representation of effective properties.
Homogenization Theory of periodic composites: multiscale asymptotic expansions applied to linear, elliptic multiscale problems (conduction, elasticity).
Exactly soluble models. Optimal bounds and the concentric shell model. Convergence properties & error estimates. Correctors.
Generalizations: reiterated homogenization, perforated microstructures, Robin boundary conditions, evolution equations, fluid flow in porous media, quasi-periodic and random materials.
Part II: Numerical Simulation
Variational Formulation, Finite Element solutions.
Multiscale Finite Element Methods.
Boundary integral formulation. Application to image-based materials.
Fixed-point iteration schemes by Fast Fourier Transform.
Computational methods based on 2D or 3D digital images.
Part III: Applications
Optical/electrostatic resonance of ceramic-metal composite coatings for solar thermal technologies.
Metamaterials for electromagnetic cloaking.
Auxetic materials for electronics, bioengineering, textiles, etc.
Phononic band-gap materials for sound or vibration protection devices, frequency filters or waveguides.

Why do small drops stay attached to a windshield? While the formation of foam is a necessity in shampoos, how can it be avoided in dishwashers? How can leaves be wetted optimally during the application of insecticides while preventing the formation of drops on the soil? The answers to these questions lie in the study of interfacial phenomena, the subject of this course. Many technological and natural processes involve phenomena dominated by interfacial mechanics, such as in coating, printing, pharmaceutical, microfluidics and oil technologies, but also in the biology of the lungs or the cell. In addition to capillary, viscous and gravitational forces, interfacial phenomena involve the interplay of other complex physico-chemical processes such as intermolecular forces, surface active materials, and evaporation.
I. Capillarity: 1. Surface tension: physical origin, energy and force interpretation, physical measurement. 2. Static capillary interfaces: Laplace equation, pression discontinuity, minimal area surfaces. 3. Three-phase contact and wetting: classification of wetting behavior, the spreading parameter, Young equation and equilibrium contact angle, Zisman rule, liquid substrate.
II. Capillarity and Gravity: 1. Capillary length. 2. Shape of drops in partial wetting. 3. Meniscus: characteristic shape ans scales, meniscus on thin fiber. 4. Capillary rise in tubes. 5. Liquid lenses. 6. Stability of capillary surfaces.
III. Contact Angle Hysteresis: 1. Advancing and receding angles, hysteresis, contact line pinning. 2. Elasticity of contact line.
IV. Wetting and Intermolecular Forces: 1. Energetics of submicroscopic thin film. 2. Disjoining pressure. 3. Classification of wetting. 4. Long-range and short range molecular forces. 5. Physical manisfestation of molecular forces.
V. Interfacial Hydrodynamics of Thin Films: 1. Scales and the lubrication approximation. 2. Hydrodynamics of thin films: gravity drainage on an inclined plane, leveling of liquid interface, Rayleigh instability, Plateau-Rayleigh instability. 3. Forced wetting: Laudau-Levich and Bretherton problems, forced wetting on thin fibers. 4. Impregnation: Washburn law, corrections, inertial regime. 5. Capillary waves.
VI. Moving Contact Lines: 1. Experimental observations, dynamic contact angles, dynamic wetting transition. 2. Moving contact line singularity. 3. Contact-angle/Contact-line-velocity relations: hydrodynamic models, other models. 4. Kinetics of total wetting.
VII. Kinetics of Dewetting: 1. Experimental observations, critical thickness for dewetting. 2. Viscous regime. 3. Inertial regime. 4. Visco-elastic regime.
VIII. Surfactants: 1. Characteristic features of surfactant. 2. Structural features and behavior of Surfactants. 3. Micelle formation. 4. Adsoption of surfactant at interfaces. 5. Reduction of surface and interfacial tension by surfactants. 6. Wetting and its modification by surfactants. 7. Surfactant and soap films. 8. Application of surfactants.
IX. Other Topics: 1. Wetting on textured substrates: super-hydrophobicity. 2. Wetting and porous media. 3. Entrainment phenomena: Marangoni effects, electrocapillarity, electro-osmosis.