A three-dimensional numerical model for the motion of liquid drops by the particle finite element method

Elaf Mahrous, R. Valéry Roy, Alex Jarauta and Marc Secanell Physics of Fluids 34.5 (2022): 052120.

https://doi.org/10.1063/5.0091699

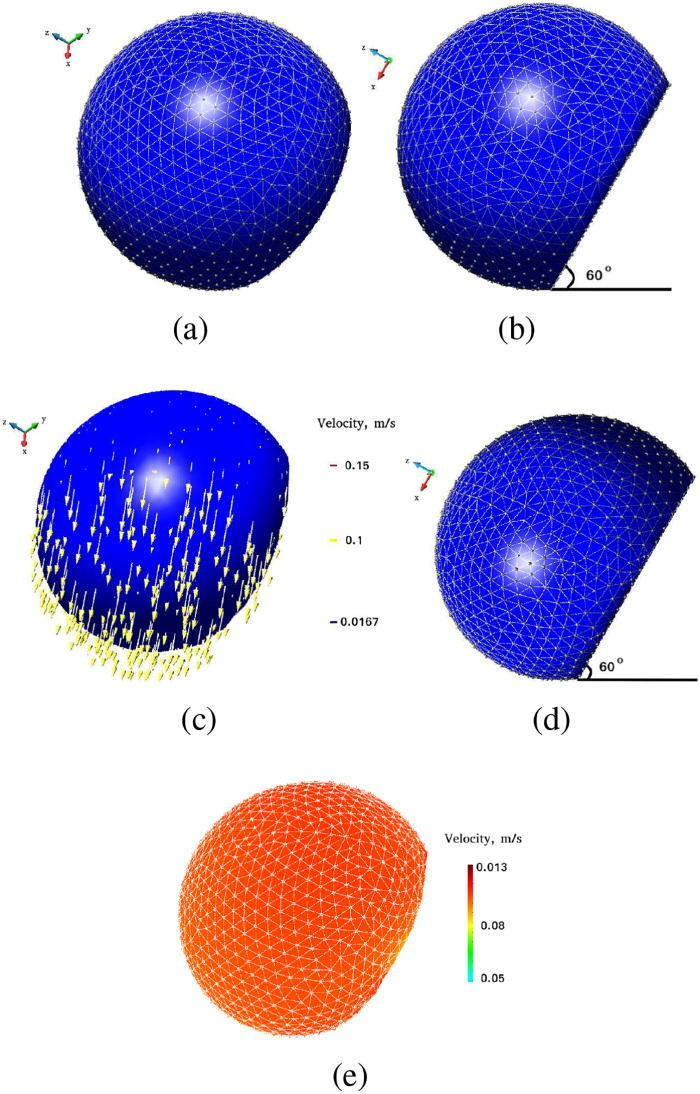
Abstract: Analysis of drop spreading and sliding on solid substrates is critical for many industrial applications, such as microfluidic devices, cooling towers, and fuel cells. A new three-dimensional model is proposed for droplet dynamics. Its numerical solution is obtained by the particle finite element method, based on an updated Lagrangian framework to accurately track the deformation of the droplet. The model hinges on boundary conditions at the solid–liquid interface to account for viscous dissipation and retention forces. These conditions are essential to obtain mesh-independent solutions and a realistic spatiotemporal evolution of the droplet deformation. Several numerical simulations are performed to assess the performance of the model for spreading and sliding drops, and results are compared to experimental data found in the literature. Good agreement is obtained with the available data. Simulations performed in two dimensions show striking discrepancies with the experimental data, thus demonstrating the need for three-dimensional simulations.