A particle finite element-based model for droplet spreading analysis

Elaf Mahrous, Alex Jarauta, Thomas Chan, Pavel Ryzhakov, Adam Z. Weber, R. Valéry Roy and Marc Secanell

Physics of Fluids 32, 042106 (2020); https://doi.org/10.1063/5.0006033

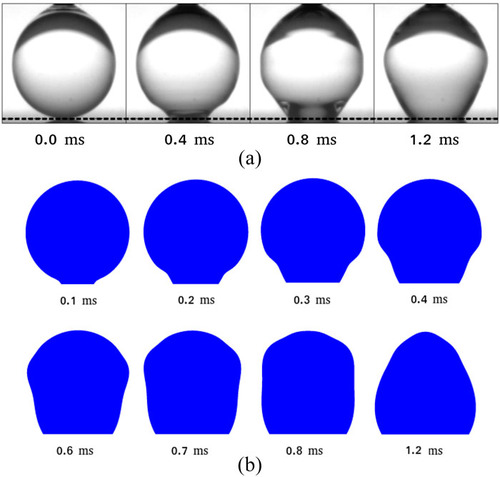
A particle finite element method-based model is proposed to analyze droplet dynamics problems, particularly droplet spreading on solid substrates (wetting). The model uses an updated Lagrangian framework to formulate the governing equations of the liquid. The curvature of the liquid surface is tracked accurately using a deforming boundary mesh. In order to predict the spreading rate of the droplet on the solid substrate and track the corresponding contact angle evolution, dissipative forces at the contact line are included in the formulation in addition to the Navier-slip boundary conditions at the solid–liquid interface. The inclusion of these boundary conditions makes it possible to account for the induced Young’s stress at the contact line and for the viscous dissipation along the solid–liquid interfacial region. These are found to be essential to obtain a mesh-independent physical solution. The temporal evolution of the contact angle and the contact line velocity of the proposed model are compared with spreading droplets and micro-sessile droplet injection experiments and are shown to be in good agreement.