Numerical computation of the effective thermal conductivity of two-phase composite materials by digital image analysis
International Journal of Heat and Mass Transfer
Volume 197, 15 November 2022, 123377
Kelechi Ogbuanu and R. Valéry Roy
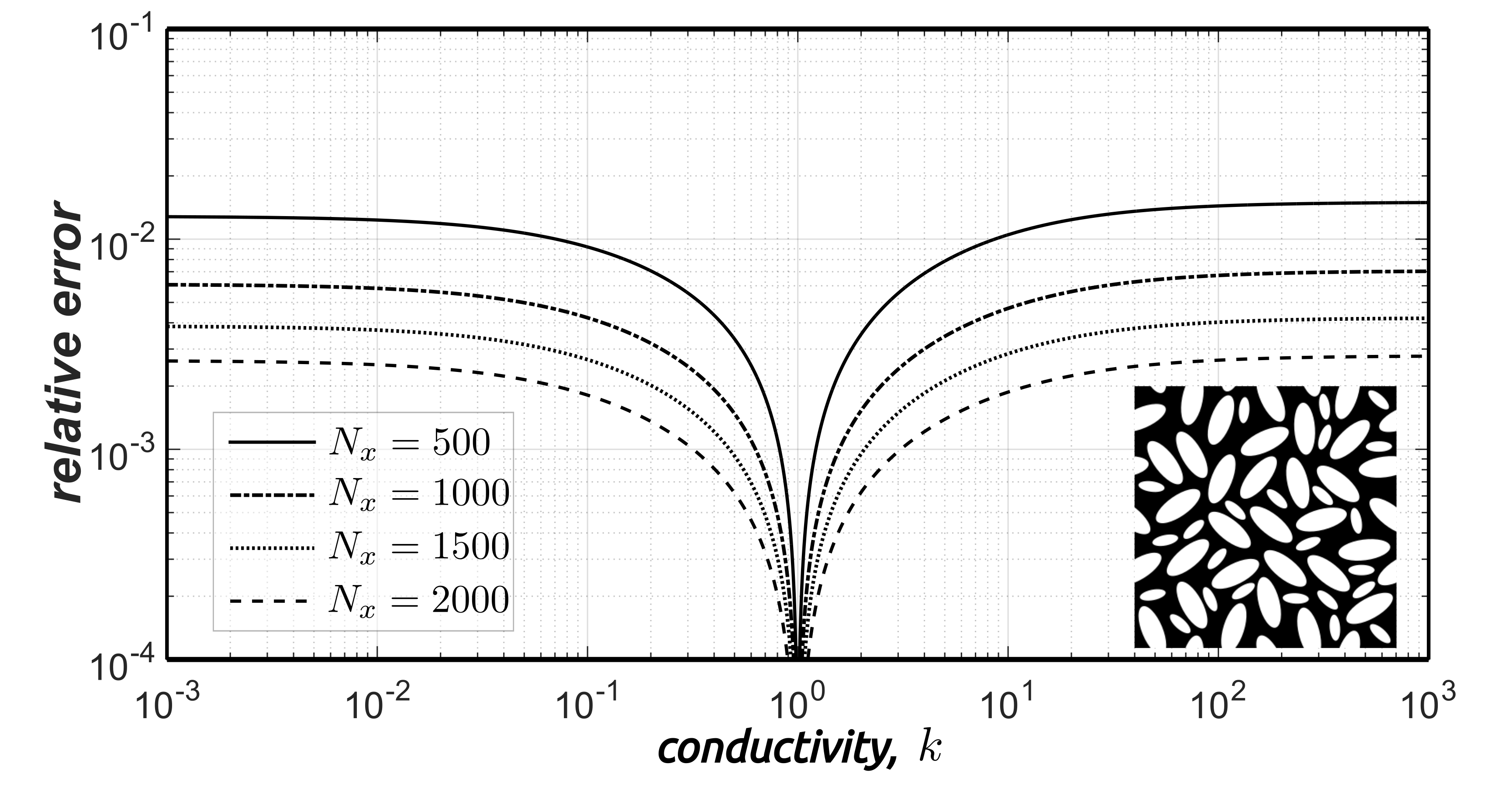
Abstract: We consider the numerical determination of the effective thermal conductivity of 2D, two-phase composite materials, whose microstructural geometries are described by digital images. More specifically, key microstructural data pertaining to the spatial distribution and volume fractions of the constituent phases in the material are extracted, along with the shapes of the interphase boundaries, using computer vision techniques. For inclusions of simple shapes (polygons, circles, ellipses), the extracted interphase boundary data is easily obtained and can be exploited immediately (e.g. polygonal vertices) or can be fitted with smooth curves, using least square error minimization techniques in order to reconstruct parametric representations in the case of circular or elliptical boundaries. For more intricate microstructure geometries characterized by clustered or agglomerated intersecting inclusions, piecewise cubic spline functions are adopted to obtain a least-square fitting of the interphase boundaries. The effective thermal conductivities are then calculated based on a boundary integral formulation defined over the reconstructed inclusion boundaries. They are expressed in terms of power series expansions of a conductivity contrast parameter of the constituent phases in the material. To accelerate the convergence of these expansions, nonlinear transformations (known as Padé Approximants) are used to yield rational approximations of the effective thermal conductivity tensor. Tests conducted on a variety of 2D, two-phase microstructures yielded accurate results over a wide range of microstructure image resolution, regardless of the contrast parameters of the constituent phases, thus, validating the efficacy and robustness of the proposed scheme.