Problem 1.
1.1. The mechanism corresponds to the closed loop \(0-1-3-2-0\). The velocity loop equation can then be stated as (choosing point \(C\)): \[ {\bf v}_{C\in 1/0} ={\bf v}_{C\in 1/3}+ {\bf v}_{C\in 3/2}+{\bf v}_{C\in 2/0} \] with
\({\bf v}_{C\in 1/0} = -v_1 \boldsymbol{\hat{\imath}}\) since the joint \(1/0\) is a slider,
\({\bf v}_{C\in 1/3} = \omega_{1/3}\boldsymbol{\hat{k}}\times {\bf r}_{IC} = -r_1 \omega_{1/3}\boldsymbol{\hat{\imath}}\), since the joint \(1/3\) is a no-slip point contact at \(I\),
\({\bf v}_{C\in 3/2} = \omega_{3/2}\boldsymbol{\hat{k}}\times {\bf r}_{JC} = r_2 \omega_{3/2} \boldsymbol{\hat{\imath}}\), since the joint \(3/2\) is a no-slip point contact at \(J\),
\({\bf v}_{C\in 2/0} = v_2 \boldsymbol{\hat{\imath}}\), since the joint \(2/0\) is a slider.
This gives a single equation (on \(\boldsymbol{\hat{\imath}}\)) \[ -v_1 = -r_1 \omega_{1/3}+r_2\omega_{3/2} + v_2 \qquad{[1]} \]
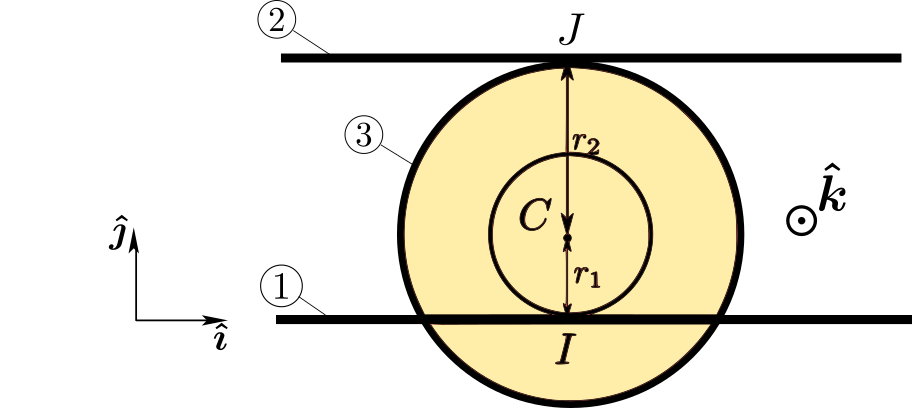
The angular velocity loop equation also gives: \[ \omega_{1/0} = \omega_{1/3}+\omega_{3/2}+\omega_{2/0} \] Since \(\omega_{1/0}= \omega_{2/0} = 0\), we obtain: \[ \omega_{1/3}+\omega_{3/2}=0 \qquad{[2]} \] Now we can solve for the 2 unknowns in the problem. We find by solving [1-2]: \[ \boxed{ \omega_{1/3}= -\omega_{3/2}= \frac{v_1+v_2}{r_1+r_2} } \]
1.2 We actually want \(\omega_{3/0}\): \[ \omega_{3/0}= \omega_{3/1}+\omega_{1/0}= -\omega_{1/3}= -\frac{v_1+v_2}{r_1+r_2} \] We cannot guarantee that C moves to the right. To find out why, we need find \({\bf v}_C\) as follows: \[ {\bf v}_C= {\bf v}_{C\in 3/0} = {\bf v}_{C\in 3/1}+{\bf v}_{C\in 1/0}= (r_1 \omega_{1/3} -v_1) \boldsymbol{\hat{\imath}} \] With the expression found for \(\omega_{3/1}\) found earlier, we obtain \[ {\bf v}_C= (r_1 \omega_{1/3} -v_1) \boldsymbol{\hat{\imath}}= \frac{r_1 v_2 -r_2 v_1}{r_1+r_2}\boldsymbol{\hat{\imath}} \] For C to move to the right, we need \[ \boxed{ \frac{v_2}{v_1} > \frac{r_2}{r_1} } \] This condition may not be satisfied.
Problem 2.
Since this method is vectorial, we choose a basis of unit vectors \((\boldsymbol{\hat{\imath}},\boldsymbol{\hat{\jmath}},\boldsymbol{\hat{k}})\). See Figure 2.
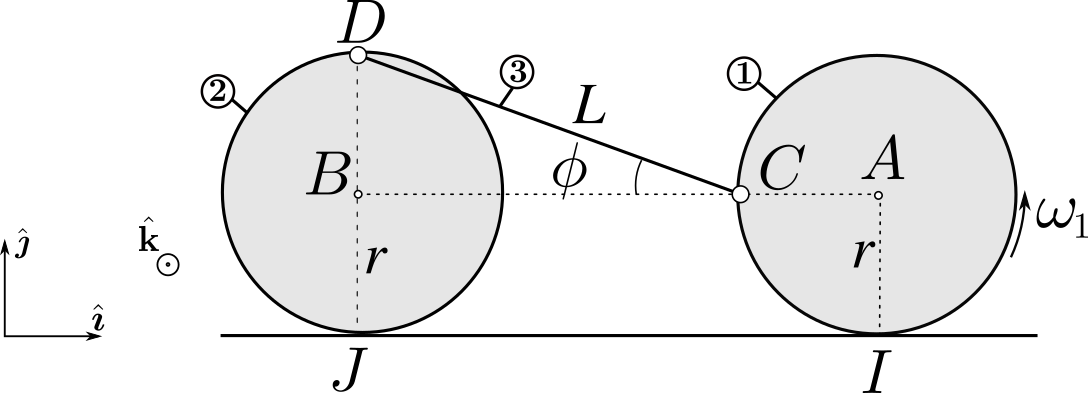
The mechanism consists of 3 rigid bodies interconnected in referential \(0\). It forms a closed loop \(0-1-3-2-0\). We can identify the nature of each joint \(i-j\) in this loop:
The joint \(0-1\) is a no-slip point contact at \(I\): for any point \(P\) we have \(\boldsymbol{v}_{P\in 1/0} = \boldsymbol{\omega}_{1/0}\times \boldsymbol{r}_{IP}\).
The joint \(3-1\) is a pivot about point \(C\): for any point \(P\) we have \(\boldsymbol{v}_{P\in 3/1} = \boldsymbol{\omega}_{3/1}\times \boldsymbol{r}_{CP}\).
The joint \(2-3\) is a pivot about point \(D\): for any point \(P\) we have \(\boldsymbol{v}_{P\in 2/3} = \boldsymbol{\omega}_{2/3}\times \boldsymbol{r}_{DP}\).
The joint \(2-0\) is a no-slip point contact at \(J\): for any point \(P\) we have \(\boldsymbol{v}_{P\in 2/0} = \boldsymbol{\omega}_{2/0}\times \boldsymbol{r}_{JP}\).
The method hinges on writing the following two loop equations: \[ \boldsymbol{\omega}_{1/0}+\boldsymbol{\omega}_{ 3/1} +\boldsymbol{\omega}_{2/3} = \boldsymbol{\omega}_{2/0} \qquad{[1]} \] \[ \boldsymbol{v}_{P\in 1/0} +\boldsymbol{v}_{P\in 3/1} +\boldsymbol{v}_{P\in 2/3} = \boldsymbol{v}_{P\in 2/0} \qquad{[2]} \] at a point \(P\) of our choice. We pick \(A\) for \(P\) (any other point will work!). We write each angular velocity \(\boldsymbol{\omega}_{i/j} = \omega_{i/j} \boldsymbol{\hat{k}}\). Recall that angular velocity \(\omega_{1/0}= \omega_1\) is given. Now equations [1-2] become (using the relationships found earlier) for each \(\boldsymbol{v}_{A\in i/j}\)): \[ \omega_{1/0}+\omega_{ 3/1} +\omega_{2/3} = \omega_{2/0} \] \[ \omega_{1/0}\boldsymbol{\hat{k}}\times (r\boldsymbol{\hat{\jmath}})+ \omega_{3/1}\boldsymbol{\hat{k}}\times (r\boldsymbol{\hat{\imath}}) + \omega_{2/3}\boldsymbol{\hat{k}}\times (-r\boldsymbol{\hat{\jmath}}+ (L\cos\phi+r)\boldsymbol{\hat{\imath}}) = \omega_{2/0} \boldsymbol{\hat{k}}\times (r\boldsymbol{\hat{\jmath}}+ (L\cos\phi+r)\boldsymbol{\hat{\imath}}) \] This yields 3 equations for 3 unknowns \((\omega_{3/1},\omega_{3/2}, \omega_{2/0})\) in terms of \(\omega_{1/0}\): \[ \begin{cases} \omega_{1/0}+\omega_{ 3/1} +\omega_{2/3} = \omega_{2/0} \\ -r\omega_{1/0} + r \omega_{2/3} = -r\omega_{2/0} \\ r\omega_{3/1} + (L\cos\phi+r) \omega_{2/3} = (L\cos\phi+r)\omega_{2/0} \end{cases} \] It is straightforward to solve these equations: \[ \boxed{\omega_{2/0}= \frac{1}{2} (1-\tan\phi) \omega_{1/0}} \] \[ \boxed{\omega_{2/3}= \frac{1}{2} (1+\tan\phi) \omega_{1/0}} \] \[ \boxed{\omega_{3/1}= - (1+\tan\phi) \omega_{1/0}} \] We can then obtain the expression of \(\boldsymbol{\omega}_{3/0}\) as follows \[ \boxed{\boldsymbol{\omega}_{3/0}= \boldsymbol{\omega}_{3/1} +\boldsymbol{\omega}_{1/0}= - \omega_{1/0} \tan\phi \boldsymbol{\hat{k}}} \]