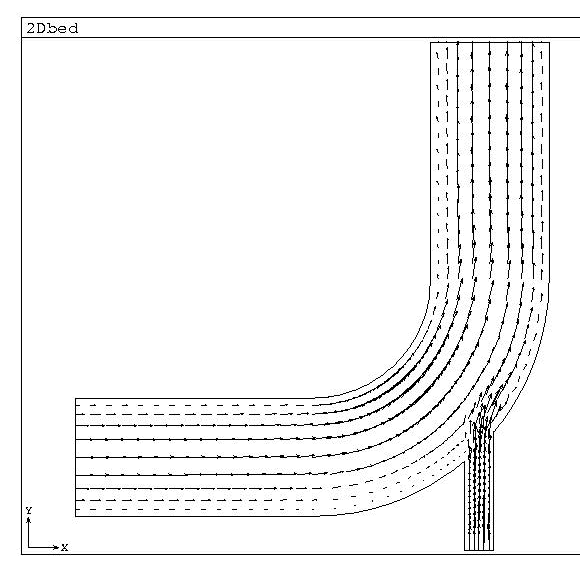
The long-time (steady-state) velocoty field
In this session we solve an unsteady flow and heat transfer in a mixing elbow using Gambit and FIDAP.
Note that the geometry dimensions are given
in inches, while other properties are in SI units.
Geometry and parameters:

The long-time (steady-state) velocoty field
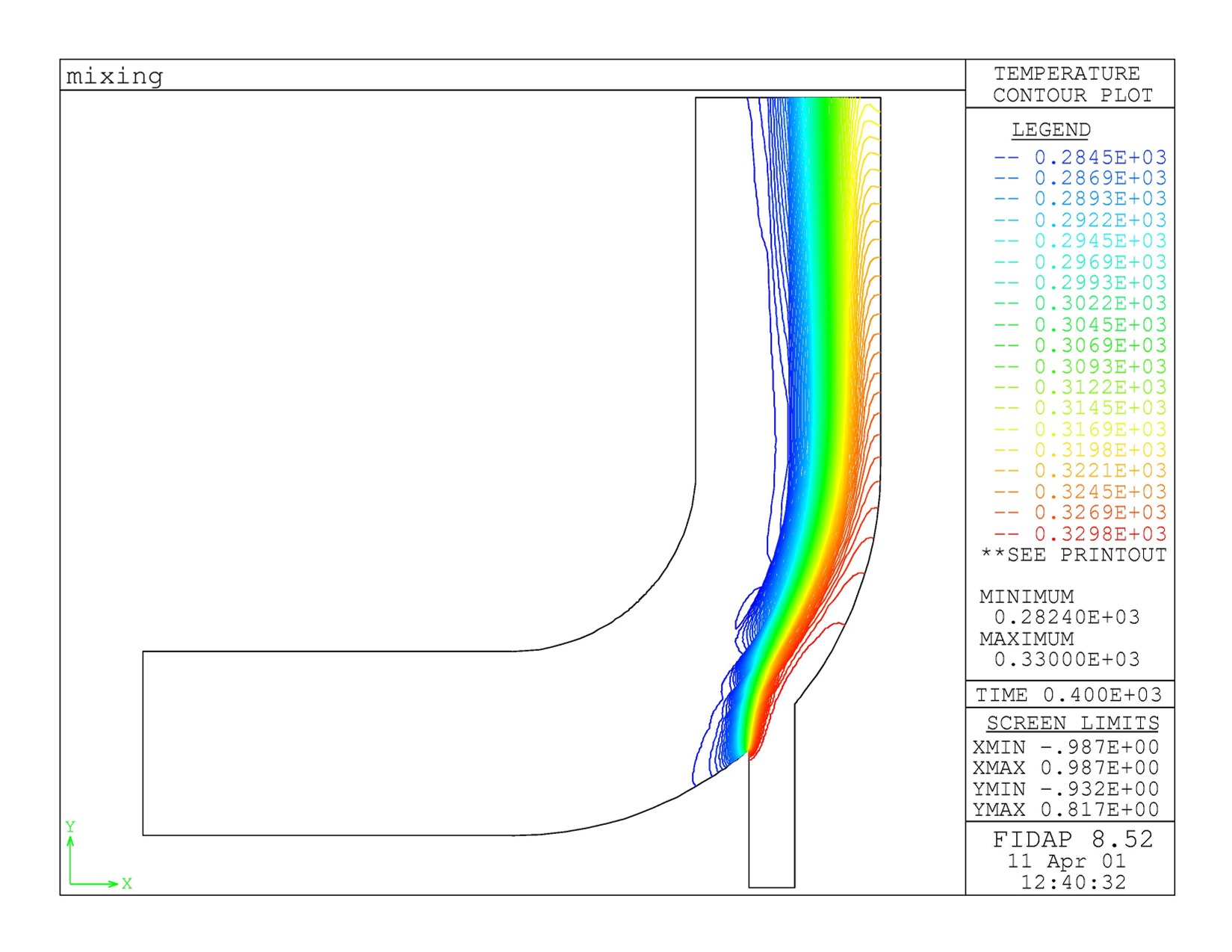
The long-time (steady-state) temperature distribution for laminar flow.
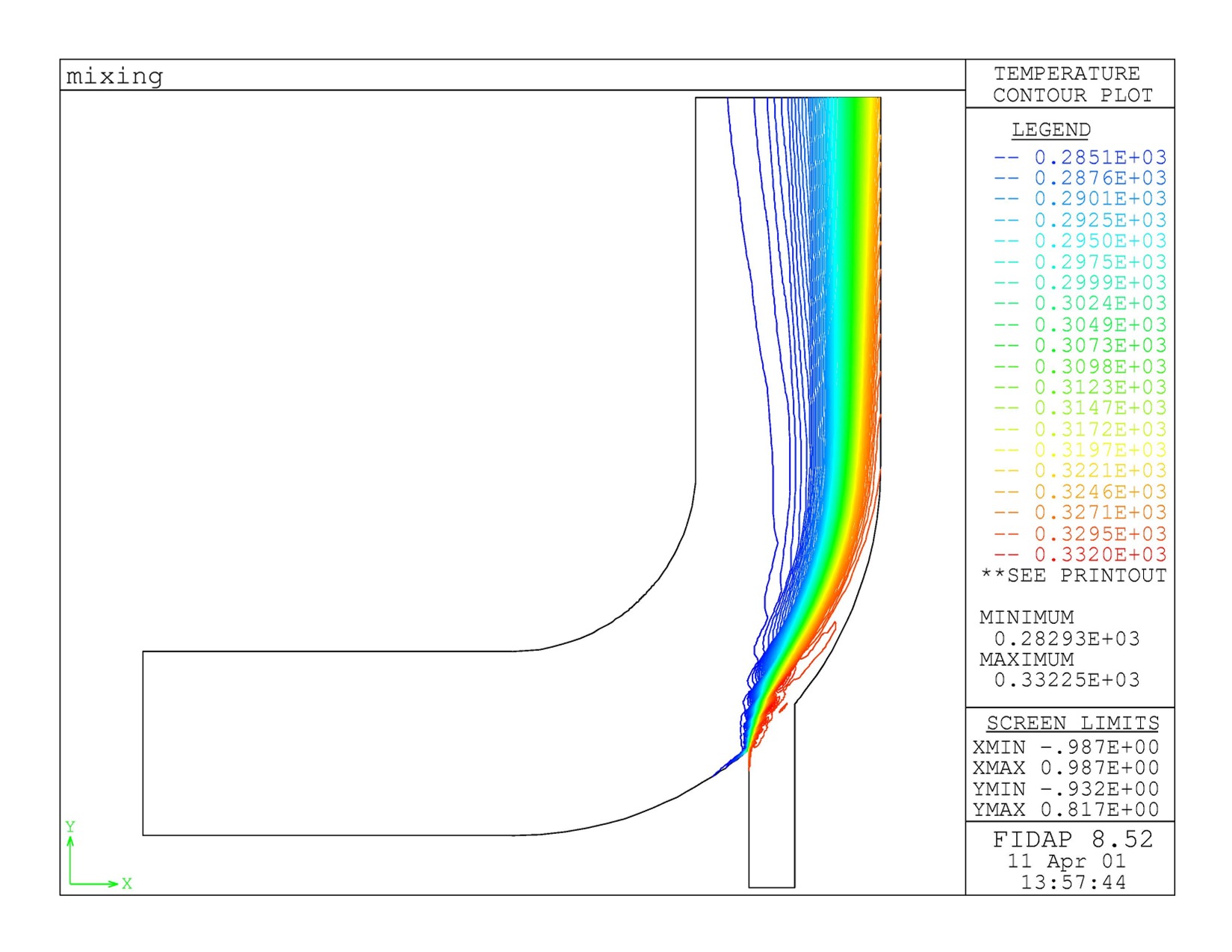
The steady-state temperature distribution for turbulent flow.
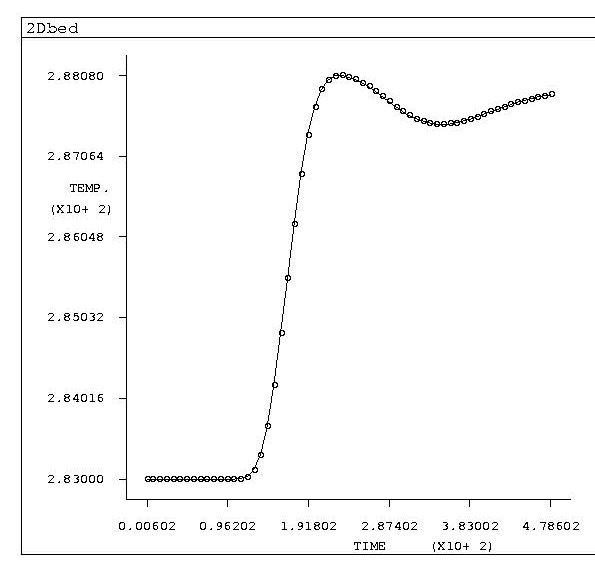
Temperature at the center of the outlet at a function of time (laminar flow).
General Instructions for Setting up the
model of mixing elbow
gambit -id mixing -dev X -new
1. Select a solver
Solver - FIDAP
2. Display 4x4 grid covering -32 < x < 32, -32 < y < 32 using
Tools - Coordinate System - Display Grid
3. Pick 9 vertices
(-32, -32) (0.,-32) (-32,-16) (0,-16)
(0., 0. ) (16, 0.) (32, 0.)
(16, 32) ( 32,32)
using Crtl + right click
4. Remove grid by deselecting Visibility
5. Create Arcs for the bend of the mixing elbow
Geometry - Edge - Create Edge - Arc
Shift + left click at point (0., 0.) !define the center
Left click End-Points field
Shift + left click at points (16,0.) (0, -16) !define end points
Apply
Repeat to create the outer arc.
6. Creat straight edges
Geometry - Edge - Create Edge - Straight
Shift + left click to select points, then apply
7. Create the small pipe for the mixing elbow
Geometry - Edge - Split/Merge Edges
Select the large arc
Type = Cylindrical
local t = -39.93
Apply
Select the larger portion of the nearly created arc
local t = -50.07
Apply
Geometry - Vertex - Move/Copy Vertices
! Make a copy of nearly created vertex by shifting in y by -12
Click Fit-to-Window
Create another vertex by copying and shifting in x by 4
Create the edges
8. Create faces from egdes
Geometry - Face - Create Face
Shift + left click each edge of teh large pipe, in turn, to form
a continuous loop
Apply
Repeat for the small pipe
9. Specify node distribution
On Inlet and Outlet of te large pipe:
Mesh - Edge - Mesg Egdes
Select inlet and outlet
Grading = Apply, Type = Successive Ratio
Ratio = 1.25
Double Sided is on
Use 10 interval counts
Apply
4 straight edges of the large pipes
use 15 equal intervals
Large arcs:
6 equal intervals for the center part
12 graded intervals, ratio =0.9
(make sure arrow pointing towards the small pipe,
Use shift-middle click to change direction)
Inner arc:
double sided, ratio = 0.85
Turn off Option / Mesh !Let gambit decide the mesh later
Apply
10. Create structured mesh:
Mesh-Face-Mesh Faces
Select the large pipe
Elements = Quad
Type = Map
11. Mesh the small pipe:
Select the small pipe
Elements = Quad
Type = Map
Spacing = 1
Apply
12. Set Boundary Types
Specify model Display Attributes - Mesh = off - Apply
Zones - Specify boundary types
name = inflow1, type = plot, Entity/Edges (select large pipe inlet), Apply
name = outflow, type = plot, Entity/Edges (select large pipe outlet), Apply
name = inflow2, type = plot, Entity/Edges (select small pipe inlet), Apply
name = walls, type = plot, Entity/Edges (select all wall edges), apply
13. Export neutral file
Export - Mesh - Accept
14. Exit - Save
This will generate:
*.jou: a journal file
*.trn: a summary file
*.FDNEUT: a neutral file
*.FIPREP: FIPREP file
15. Start fidap: fidap -id mixing -gui -new
Read mixing.FIPREP
16. Set up boundary and initial conditions according to the following:
/
FIPREP
PROB (2-D, INCO, TRAN, LAMI, NONL, NEWT, MOME, ENER, FIXE, NOST, NORE, SING)
EXEC (NEWJ)
SOLU (S.S. = 20, VELC = 0.100000000000E-02, RESC = 0.100000000000E-02,
ACCF = 0. )
/
TIME (BACK, NSTE = 400, TSTA = 0. , DT = 0.1, TEND=800., VARI, WIND, NOFI, DTMA = 2.0)
DATA (CONT)
/ Define a second coordinate system centered at large pipe inlet, Mesh Data - Coordinate
COOR (SYST = 2, CART)
-0.3200000000E+02, -0.2400000000E+02, 0.0000000000E+00
PRIN (NONE)
/ Save the results every 4 steps
POST (NBLO = 1, NOPT, NOPA)
4, 400, 4
/ convert inch to m by SCAL, Mesh Data - Scale
SCAL (VALU = 0.254000000000E-01)
ENTI (NAME = "fluid", FLUI)
ENTI (NAME = "inflow1", PLOT)
ENTI (NAME = "inflow2", PLOT)
ENTI (NAME = "outflow", PLOT)
ENTI (NAME = "walls", PLOT)
DENS (SET = 1, CONS = 1.18)
VISC (SET = 1, CONS = 0.184000000000E-04)
SPEC (SET = 1, CONS = 1005.0)
COND (SET = 1, CONS = 0.260000000000E-01)
BCNO (UX, ENTI = "inflow2", ZERO)
BCNO (UY, ENTI = "inflow2", CONS = 0.100000000000E-01, EXCL)
BCNO (TEMP, ENTI = "inflow2", CONS = 330.0, EXCL)
BCNO (UX, ENTI = "inflow1", POLY = 1, SYST = 2, CART)
0.1000000000E-01, -0.1562500000E-03, 0.0000000000E+00, 0.2000000000E+01,
0.0000000000E+00
BCNO (UY, ENTI = "inflow1", ZERO)
BCNO (TEMP, ENTI = "inflow1", CONS = 283.0)
BCNO (VELO, ENTI = "walls", ZERO, X, Y, Z)
/ The walls are adiabatic by default
ICNO (VELO, ZERO, ENTI = "fluid", X, Y, Z)
ICNO (TEMP, CONS = 283.0, ENTI = "fluid")
END
17. Run and postprocessing
You can use Utility/Timestep to select the time step for displaying the results.
Plot / History can be used to plot time-evolution results at any node.
Turbulent Flow:
Lecture on turbulence modeling
The inlet velocity is assumed to be 10 m/s at both inlets. two-equation k.e.-dissipation
model is used. The boundary conditions for k.e. and dissipation are: k.e. = 0.035 u^2, diss = 0.01 u^3/D.
FIPREP
PROB (2-D, INCO, STEA, TURB, NONL, NEWT, MOME, ENER, FIXE, NOST, NORE, SING)
PRES (PENA = 0.100000000000E-07, DISC)
EXEC (NEWJ)
SOLU (S.S. = 100, VELC = 0.100000000000E-02, RESC = 0.100000000000E-02,
ACCF = 0.4)
DATA (CONT)
OPTIONS(UPWINDING)
UPWINDING
1 1 0 0 2 0 1 1
PRIN (NONE)
SCAL (VALU = 0.254000000000E-01)
ENTI (NAME = "fluid", FLUI)
ENTI (NAME = "inflow1", PLOT)
ENTI (NAME = "inflow2", PLOT)
ENTI (NAME = "outflow", PLOT)
/
ENTI (NAME = "walls", WALL)
/ Here the ENTITY Type = WALL is very important, so that the walls will be treated with special wall elements
/ in the turbulence modeling
/
TURBCONSTANTS
0 0 0 0 0 0 0.9
/ Turbulent Prandtl number = 0.9, Other model constants are set to default
DENS (SET = 1, CONS = 1.18)
VISC (SET = 1, CONS = 0.184000000000E-04, TWO-)
SPEC (SET = 1, CONS = 1005.0)
COND (SET = 1, CONS = 0.260000000000E-01)
BCNO (UX, ENTI = "inflow2", ZERO)
BCNO (UY, ENTI = "inflow2", CONS = 10.0, EXCL)
BCNO (TEMP, ENTI = "inflow2", CONS = 330.0, EXCL)
/ k.e. = 0.035 u^2 , diss = 0.01 u^3/D
/
BCNO (KINE, ENTI = "inflow2", CONS = 3.5)
BCNO (DISS, ENTI = "inflow2", CONS = 98.4)
/
BCNO (UY, ENTI = "inflow1", ZERO)
BCNO (UX, ENTI = "inflow1", CONS = 10.0, EXCL)
BCNO (TEMP, ENTI = "inflow1", CONS = 283.0)
BCNO (KINE, ENTI = "inflow1", CONS = 3.5)
BCNO (DISS, ENTI = "inflow1", CONS = 24.6)
/
BCNO (VELO, ENTI = "walls", ZERO, X, Y, Z)
ICNO (VELO, ZERO, ENTI = "fluid", X, Y, Z)
ICNO (TEMP, CONS = 283.0, ENTI = "fluid")
ICNO (KINE, CONS = 3.5, ENTI = "fluid")
ICNO (DISS, CONS = 24.6, ENTI = "fluid")
END