Objectives:
Important things to know about ANSYS:
ansys -g -j jobname
For other start-up options,
see Chapter 3 of Operation Guide.
--------------------------------------------------------
FILE TYPE FILE NAME FILE FORMAT
Log file jobname.log ASCII
Error file jobname.err ASCII
Output file jobname.out ASCII
Database file jobname.db Binary
Results file: Binary
Solid/Structural jobname.rst
Thermal jobname.rth
Fluid jobname.rfl
------------------------------------------------------
The log file is the most important file. It keeps a complete log
of an ANSYS session (list all commands you execute). You can
read the log file, view it while in ANSYS, edit it,
and input it later.
Note: use ! for comments
To input a log file: FILE - Read input from ...
The error file lists all the errors and warnings. You may use
this to edit your log file.
Output file:
containing:
-- Load summary information,
-- mass and moments of inertia of the model
-- solution summary information
-- total CPU time,
-- data requested by the OUTPR output control command
e.g., General Postprocesser - list results - modal -
- print output
If you run the solution interactively, the output
file is actually your screen (window). By doing the following
before issuing SOLVE, you can divert the output
to a file instead of the screen:
File - Switch Output to - File
Database file: Contains all model information
Results file: contains solution data generated during SOLVE steps
PlotCtrls - Style - Size and Shape Plot - Elements
-- graphical display: contour, deformed shape, reaction force.. -- tabular listings (can be saved in the output file)
(1) PlotCtrls: changing graphics specifications
Plot: select graphics action
(2) Replot and Erase:
Plot - Replot
PlotCtrls - Erase Options - Erase Screen
(3) Multi-Plotting Techniques
(a) PlotCtrls - MultiWindow Layout
(b) PlotCtrls - Multi-Plot Controls
(4) Storing a graphics display on a file:
PlotCtrls - Redirect Plots - to Graphics File
Two-dimensional modeling of the Steel Plate using ANSYS
You can use ANSYS to answer the question:
To what extent is one-D solution adequate?
The two-D solid-element model for the Steel Plate problem:
Mesh resolution: 32x8, namely 32 elements in X and 8 elements in Y
Objective: (1) Study the effect of external load distribution
(2) Study the effect of different Poisson ratio
Model Development (for Poisson ratio=0.3, Load over 1/2 of width):
ansys -g -j 2Dsolid &
1. Set Preference:
Preferences - Structural = on - OK
2. Key Points:
Preprocessor - Modeling.Create - Keypoints - In Active CS
Keypoint number = 1, X,Y,Z = 0., -3., 0. -- > Apply
Keypoint number = 2, X,Y,Z = 0., 3., 0. -- > Apply
Keypoint number = 3, X,Y,Z = 24, 1.5, 0. -- > Apply
Keypoint number = 4, X,Y,Z = 24, -1.5, 0. -- > OK
3. Lines:
Preprocessor - Modeling.Create - Lines/lines - Straight line
Now left click points 1 and 2;
Then left click points 2 and 3;
Then left click points 3 and 4;
Then left click points 4 and 1;
-> Cancel
4. Surface:
Preprocessor - Modeling.Create - Areas/Arbitrary - By lines
Pick (by left click) the four lines
Apply - Cancel
5. Define materials
Preprocessor - Material props - Material models
- Structural - Linear - Elastic - Isotropic - OK
Young's modulus EX = 30e6
Poisson's Ratio PRXY = 0.3
- Density
Density DENS = 0.2836
OK
Material - Exit
6. Select Mesh Type:
Preprocessor - Element Type - /Add/edit/Delete - Add
Select "Structral Solid" and "Quad 4node 42"
OK
Options - Element behavior = Plane strs w/thk - OK
Close
Preprocessor - Real Constants - /Add/edit/Delete - Add - OK
THK = 1.0 - OK - Close
7. Meshing:
Preprocessor - Meshing/size Cntrls - Lines/Picked lines
Pick two long lines - Apply - NDIV = 32 - OK
Preprocessor - Meshing/size Cntrls - Lines/Picked lines
Pick two short lines - Apply - NDIV = 8 - OK
Close "the size Cntrls window"
Preprocessor - Meshing/Mesh - Areas/Free
Pick the area - OK
8. Apply BCs and loads:
Solution -Loads/Apply - Displacement - On nodes
Pick all the nodes at x=0
OK - Lab2 = All DOF & Value =0.0 - OK
Solution -Loads/Apply - Force/Moment - On nodes
Pick the three nodes in the middle at x=12
OK
Lab = FX, Value = 25 - OK
Solution -Loads/Apply - Force/Moment - On nodes
Pick the two nearby nodes at x=12
OK
Lab = FX, Value = 12.5 - OK
Solution -Loads/Apply - Gravity
ACELX= - 1.0, ACELY=0.0, ACELZ=0.0
OK
PlotCtrls/numbering - NODE=on - OK
Plot/nodes
PlotCtrls/Pan,Zoom,Rotate
(To zoom into x=12. This allows me to find out the node numbers at x=12)
9. Solve:
Solution - Solve/Current LS - OK - Close - Close
10. See the solution:
Select - Nodes/By number/Pick - Input 189,46, Return - OK
General Postproc - List Results - Nodal Solution
OK
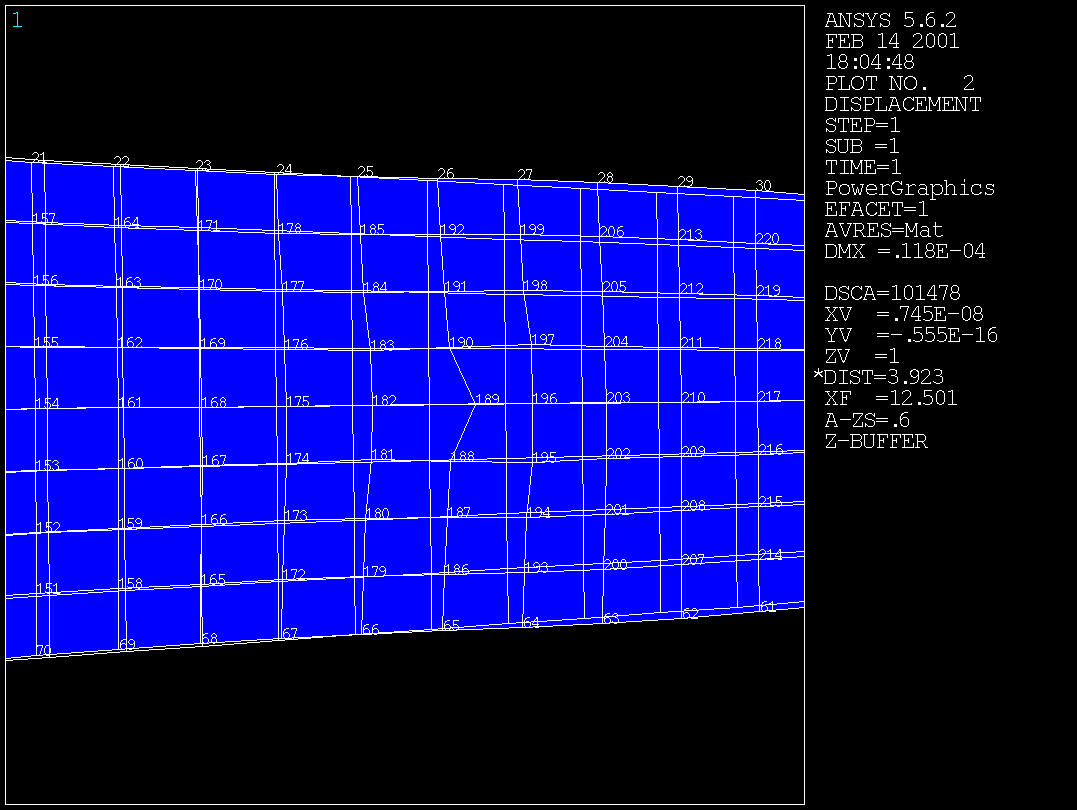
Plot Results - Deformed Shape - Def + undeformed
Modify the load distribution or the poisson ratio to see how the results vary.

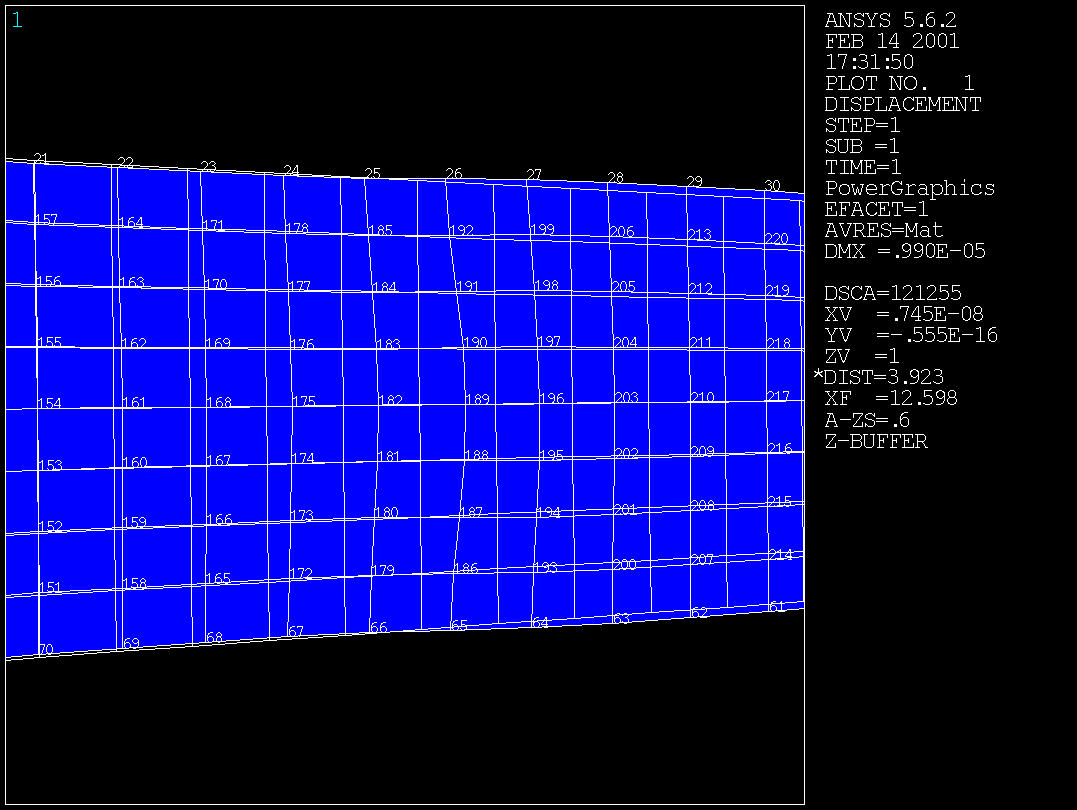
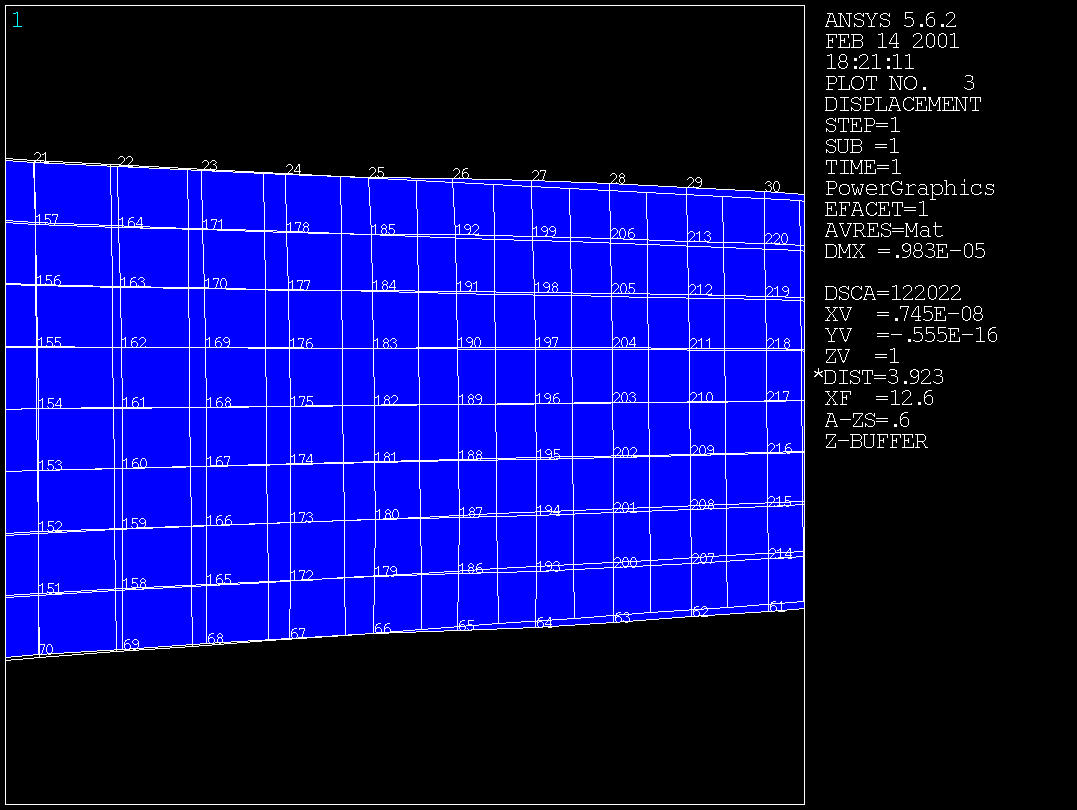
| Load distribution / Poission Ratio | Displacement at x=12 and y=0 (Node 189) | Displacement at x=24 and y=0 (Node 46) |
| 1/8 Width / 0.3 | 11.825e-6 | 9.8755e-6 |
| 1/4 Width / 0.3 | 10.601e-6 | 9.8717e-6 |
| 1/2 Width / 0.3 | 9.8965e-6 | 9.8642e-6 |
| Full Width / 0.3 | 9.2886e-6 | 9.8343e-6 |
| 1/8 Width / 0.0 | 11.488e-6 | 9.9281e-6 |
| 1/4 Width / 0.0 | 10.420e-6 | 9.9248e-6 |
| 1/2 Width / 0.0 | 9.8126e-6 | 9.9183e-6 |
| Full Width / 0.0 | 9.3139e-6 | 9.8922e-6 |
| 1D Links (2) | 9.2720e-6 | 9.9527e-6 |
| 1D analytical solution | 9.2707e-6 | 9.8684e-6 |
Two-dimensional modeling of heat conduction using ANSYS

Consider heat conduction in an aluminum plate (12in x 12in x 2in thick or 30.5 cm x 30.5 cm x 5.1 cm) subject to the following boundary conditions: Two edges are heated using thermally bonded electrical resistance strip heaters (assume constant heat flux boundary condition) The other two edges are cooled using thermally bonded heat exchanger plates supplied with cooling water from a chiller (assume constant temperature boundary condition) The bottom face is insulated with glass wool The top face is separated from the surroundings by an air gap trapped underneath a glass plate Assume: T1 = 20 C, T2=30 C, q1 = 10000 W/m^2, q2=15000 W/m^2. Material properties: conductivity = 200 W/m.k. Treat this as a 2D heat conduction problem. Solve for temperature distribution.Here are the steps for setting up the model:
Model Development:
ansys -g -j thermal &
1. Set Preference:
Preferences - Thermal = on - OK
2. Define a square region:
Preprocessor - Modeling.Create - Rectangle - By Dimension
X1=0.,X2=0.305
Y1=0.,Y2=0.305
OK
3. Define materials
Preprocessor - Material props - isotropic - OK
Thermal conductivity = 200.0
OK
4. Select Mesh Type:
Preprocessor - Element Type - /Add/edit/Delete - Add
Select "Thermal Solid" and "Quad 4node 55"
OK
Close
5. Meshing:
Preprocessor - MeshTool -
Size controls/ lines/Set -
Pick x=0 and y=o lines - NDIV = 16 - OK
set Mesher = Map
Mesh - Pick the area - OK
6. Apply BCs and loads:
Solution - Loads/Apply - Temperature - On Lines
Left click the x=L line - OK
Value = 20 - OK
On Lines - Left click the y=L line - OK
Value = 30 - OK
Loads/Apply - Heat Flux - On lines
Left click the x=0 line - OK
Value = 10000 - OK
On Lines - Left click the y=0 line - OK
Value = 15000 - OK
7. Solve
Solution - Solve/Current LS - OK
8. Plot temperature distribution on a line for comparison
with analytical solution
Define a path:
-------------
General Postproc>Path Operations>Define Path>By location>Name=y0.25, nDiv=16,OK
>NPT=1, X=0.,y=0.25, z=0, OK> NPT=2, X=.305,y=0.25, z=0, OK> Cancel
Map the variable to be plotted on the path:
------------------------------------------
General Postproc>Path Operations>Map onto Path>Lab=T, Selection=Temperature>OK
Plot the results:
------------------
Utility Menu>Plot>Results>Path Plot>Select T>OK
Save the data for comparision with analytical results:
------------------------------------------------------
Utility Menu>List>Results>Path Data>Select XG,T>OK
File>Save as>results16.dat>OK>close
9. Contour plot
General Postproc>Plot Results>Contour Plot/Nodal Solu >OK
Note: For line contours, use
/show,x11,,1
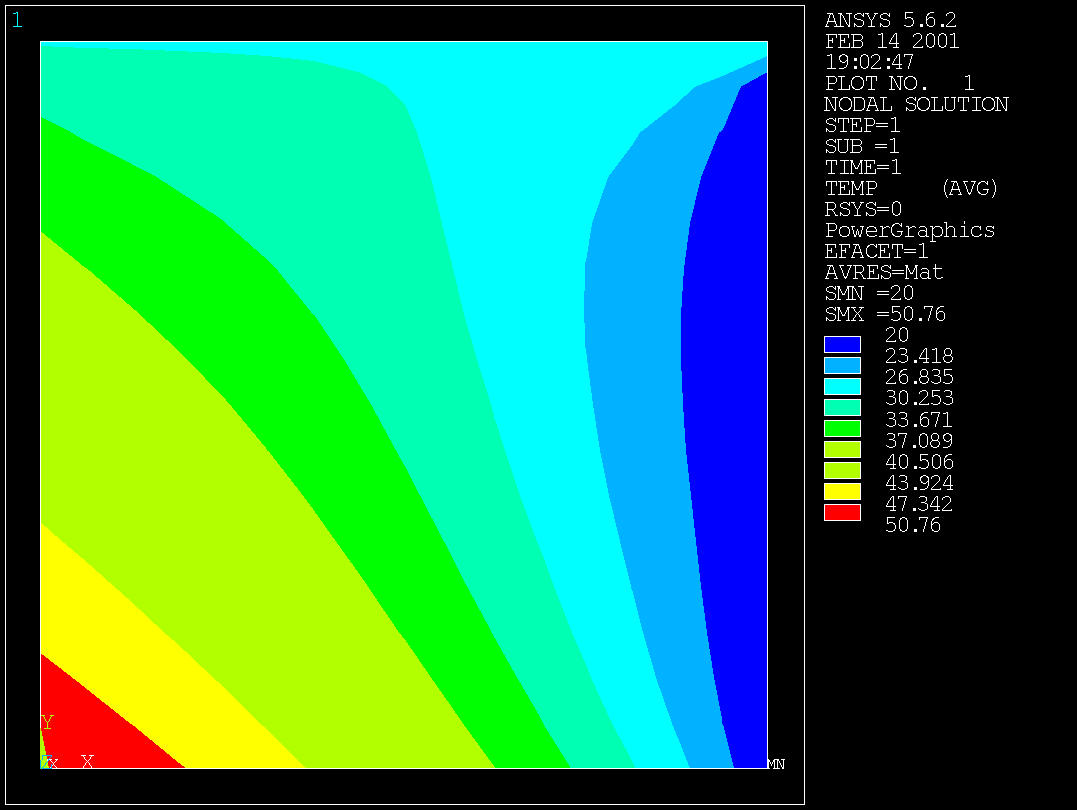 Note that you can perform a full three-D solution with ANSYS and compare
that with the 2D results.
Note that you can perform a full three-D solution with ANSYS and compare
that with the 2D results.