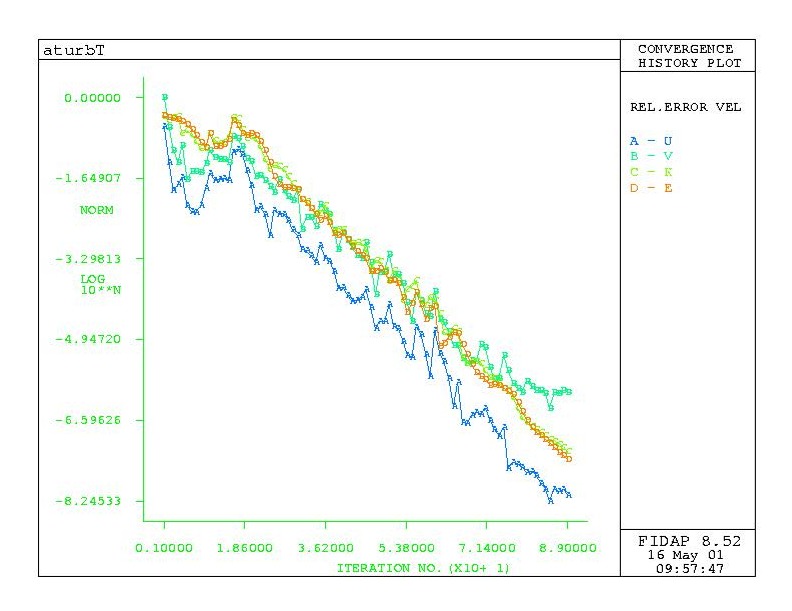
Figure 1: Convergence history
Project Presentations: Wednesday, May 23nd, 11:00 AM, 115 Gore
Back to Simple Problems - Important Physical Insights
In this session we will demonstrate how to couple physical insights of a problem with FIDAP solutions. The case problem is the study of friction and heat transfer in fully developed flows through tubes and channels.
Cross-flow diemnsion = 1, mean velocity = 1, density=1
conductivity = 1, specific heat = 1, wall heat flux = 1
Viscosity = 1/Re
Laminar flow in a circular pipe - GAMBIT file , FIDAP file
Laminar flow in a 2-D channel - FIDAP file
Turbulent flow in a circular pipe - Gambit file, FIDAP file
Important physical insights which allow us to check
and interpret our laminar flow solutions
| Laminar flow in a circular pipe | Laminar flow in a 2D channel | |
| Pressure gradient (normalized) | - 32/Re | - 12/Re |
| Surface to volume ratio | 2/R = 4 (R is pipe radius) | 1/b = 2 (b is half the channel gap) |
| dT/dx (under unit wall heat flux) | 4 | 2.0 |
Turbulent flow: pressure drop or the friction factor
Three Reynolds numbers are studied: Re= 10,000, e= 100,000 and Re= 1,000,000
Build a good mesh: What is a good mesh?
What should be the size of the computational domain?
Different mesh distribution:
/ Re = 10 K
edge mesh "edge.3" "edge.2" firstlast ratio1 0.3 intervals 8
/ Re = 100 K
edge mesh "edge.3" "edge.2" firstlast ratio1 5 intervals 20
/ Re = 1000 K
edge mesh "edge.3" "edge.2" firstlast ratio1 69 intervals 20
Check y+ for the wall layer: the good range is 30 to 300.

Figure 1: Convergence history
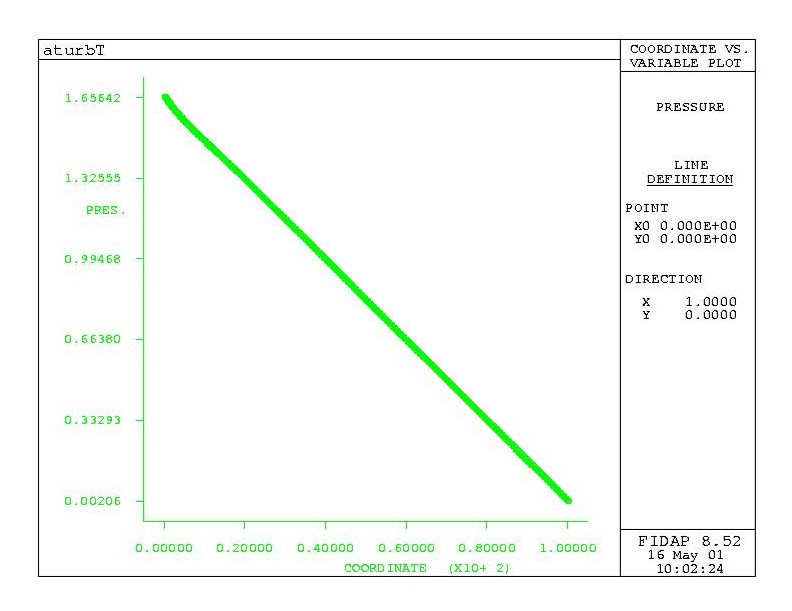
Figure 2: pressure on centerline
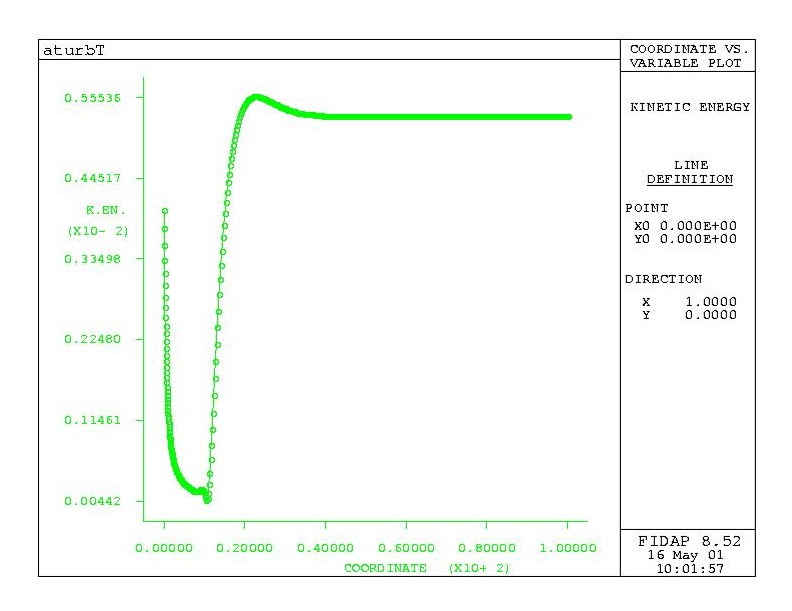
Figure 3: K.E. on centerline
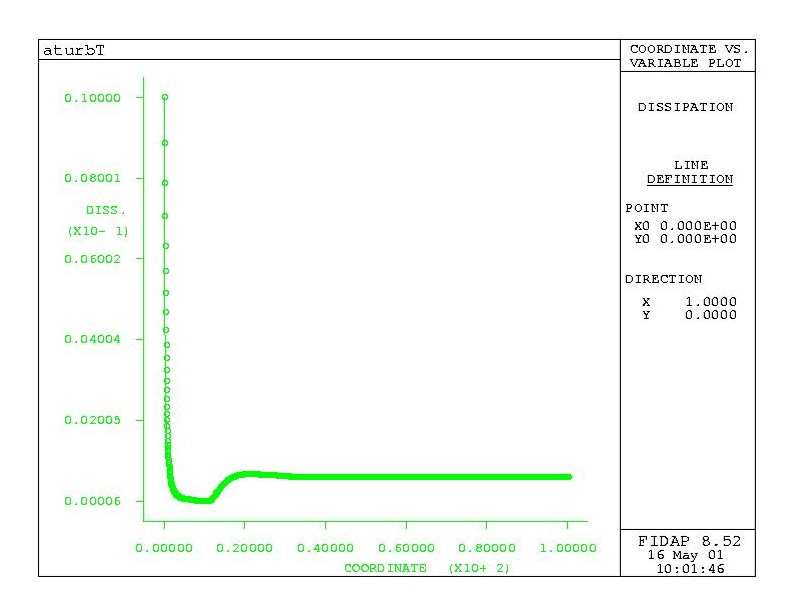
Figure 4: Dissipation rate on centerline
How good is the result?
COMPARISON OF FRICTION FACTOR
===================================
Re Observation FIDAP % error y+
100 0.64 0.6394 -0.09%
1,000 0.064 0.06403 +0.05%
10,000 0.0309 0.0328 +6.1% 32 to 55
100,000 0.0178 0.0190 +6.7% 32 to 45
1,000,000 0.0116 0.0123 +6.0% 49 to 62
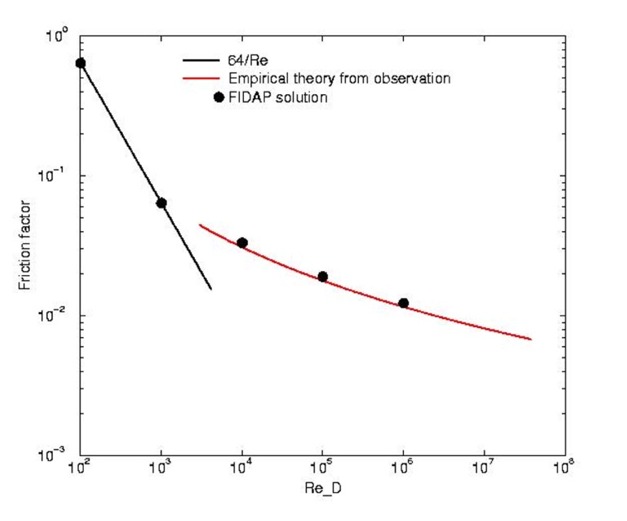
Friction factor: Comparing FIDAP solutions with observations
Comparing profiles at different Reynolds numbers
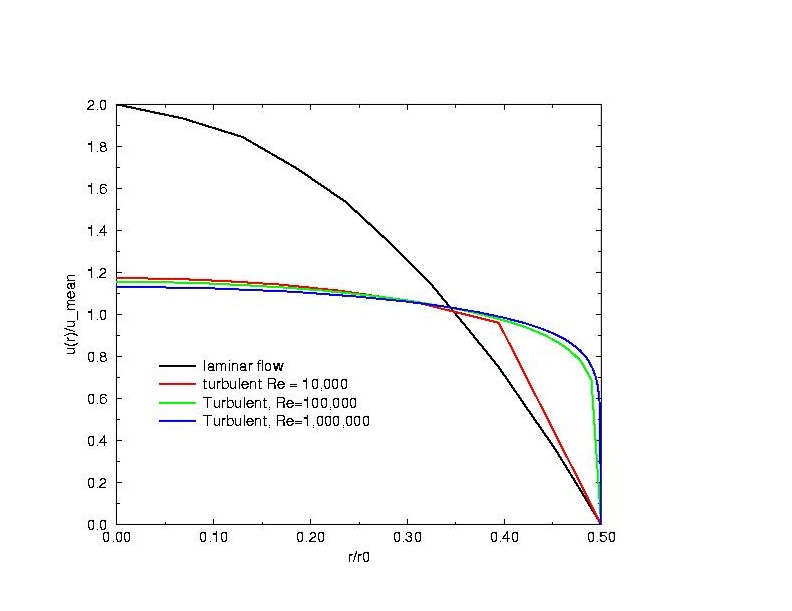
Mean velocity
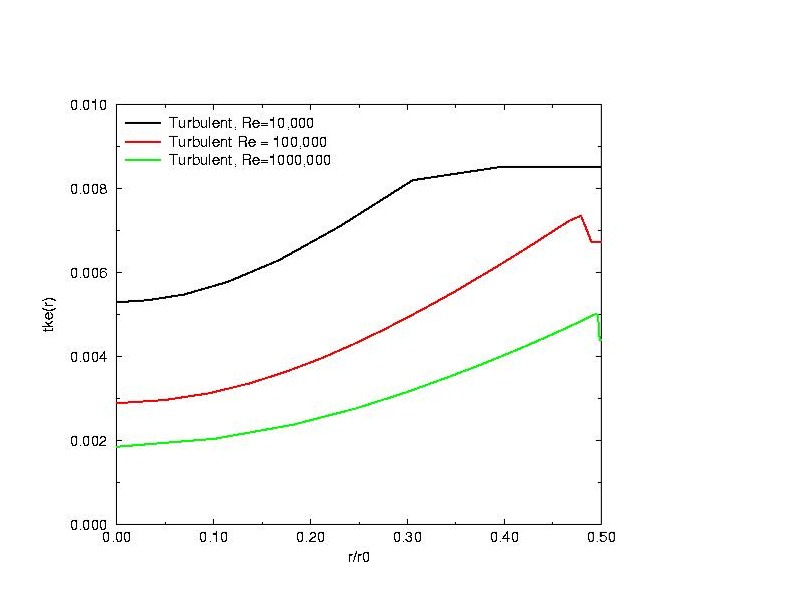
Turbulent kinetic energy
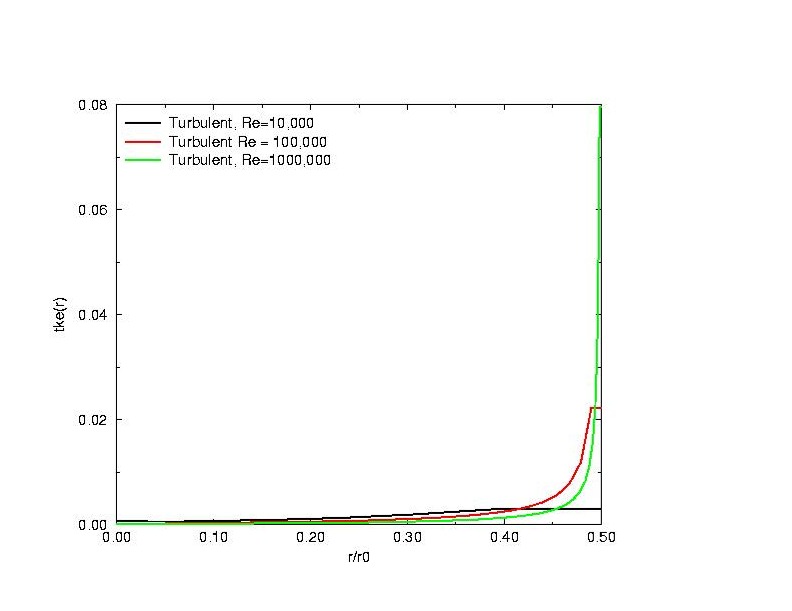
Turbulent dissipation rate
Transient laminar pipe flow driven by pressure gradient
Analytical solution in terms of Bessel functions
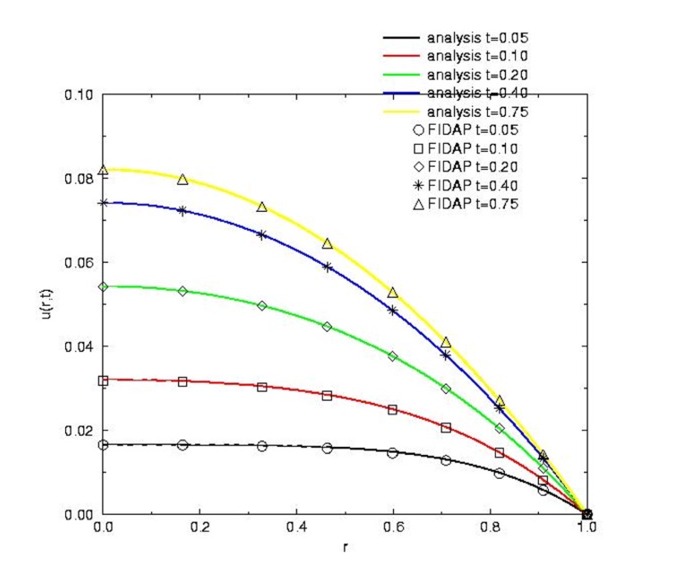
Velocity Profiles
The message of the course